题目内容
【题目】已知,![]() 的半径为1;直线
的半径为1;直线![]() 经过圆心
经过圆心![]() ,交
,交![]() 于
于![]() 、
、![]() 两点,直径
两点,直径![]() ,点
,点![]() 是直线
是直线![]() 上异于
上异于![]() 的一个动点,直线
的一个动点,直线![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是直线
是直线![]() 上另一点,且
上另一点,且![]() .
.
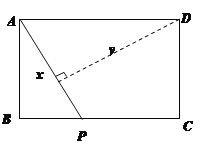
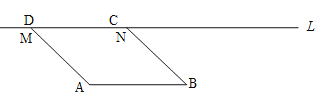
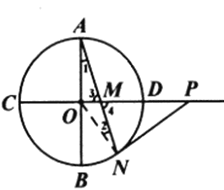
(Ⅰ)如图1,点![]() 在
在![]() 的内部,求证:
的内部,求证:![]() 是
是![]() 的切线;
的切线;
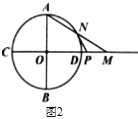
(Ⅱ)如图2,点![]() 在
在![]() 的外部,且
的外部,且![]() ,求
,求![]() 的长.
的长.

【答案】(Ⅰ)证明见解析;(Ⅱ)OP=![]() .
.
【解析】
(Ⅰ)连接ON,根据等边对等角即可证得∠1=∠2,∠PNM=∠4,然后根据直角三角形两锐角互余即可证得∠PNO=90°,即可得结论;(Ⅱ)连接ON,由∠3=30°可得∠1=60°,即可证明△AON是等边三角形,可得∠5=30°,根据等腰三角形的性质可得∠3=∠4=30°,进而可证明∠PNO=90°,利用∠3的余弦值求出OP的长即可.
(Ⅰ)如图,连接ON,
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,即
,即![]() .
.
又∵![]() 是半径,点
是半径,点![]() 在
在![]() 上,
上,
∴![]() 是
是![]() 的切线.
的切线.
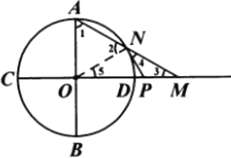
(Ⅱ)解:如图,∵![]() ,
,
∴![]()
∵ON=OA,
∴![]() 是等边三角形.
是等边三角形.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴∠OPN=60°,
∴![]() .
.
∴![]() .
.

练习册系列答案
相关题目