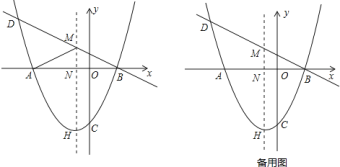
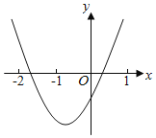
题目内容
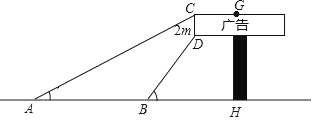
【题目】数学社团小组想利用所学的知识了解某广告牌的高度（图中GH的长），经测量知CD=2m，在B处测得点D的仰角为60°，在A处测得点C的仰角为30°，AB=10m，且A、B、H三点在一条直线上，请根据以上数据计算GH的长（
=1.73，要求结果精确得到0.1m）
【答案】GH的长约为7.7m．
【解析】
首先过点D作DE⊥AH于点E，设DE=xm，则CE=（x+2）m，解Rt△AEC和Rt△BED，得出AE=
（x+2），BE=
x，根据AE﹣BE=AB=10列出方程（x+2）﹣x=10，解方程求出x的值，进而得出GH的长.
如图，过点D作DE⊥AH于点E，设DE=xm，则CE=（x+2）m．
在Rt△AEC和Rt△BED中，有tan30°=
，
tan60°=
，
∴AE=（x+2），BE=x，
∵AE﹣BE=AB=10，
∴（x+2）﹣x=10，
∴x=5﹣3，
∴GH=CD+DE=2+5﹣3=5﹣1≈7.7（m）．
答：GH的长约为7.7m．
练习册系列答案
相关题目
