题目内容
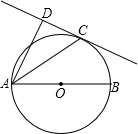 (2012•镇江二模)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
(2012•镇江二模)如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.(1)求证:AD⊥DC;
(2)若AD=
| 5 |
分析:(1)连接OC.利用等腰△AOC的两个底角相等证得∠CAO=∠OCA.然后角平分线的性质推知∠DAC=∠CAO,则内错角∠DAC=∠OCA,所以AD∥OC;最后由切线的性质证得结论;
(2)连接BC.在直角△ADC中利用勾股定理求得AC=3.然后通过相似三角形△ADC∽△ACB的对应边成比例求得AB=
;由角平分线线的性质知∠DAC=∠CAO,则sin∠CAB=sln∠DAC=
=
.
(2)连接BC.在直角△ADC中利用勾股定理求得AC=3.然后通过相似三角形△ADC∽△ACB的对应边成比例求得AB=
9
| ||
| 5 |
| DC |
| AC |
| 2 |
| 3 |
解答: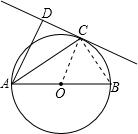 (1)证明:连接OC.
(1)证明:连接OC.
∵OC=OA,
∴∠CAO=∠OCA.
又∵AC平分∠DAB,
∴∠DAC=∠CAO,
∴∠DAC=∠CAO,
∴AD∥OC.
又∵直线CD与⊙O相切于点C,
∴∠OCD=90°,
∴∠ADC=90°,即AD⊥DC;
(2)解:连接BC.
由(1)知,∠ADC=90°,
∴根据勾股定理知,AC=
=3.
∵AB为圆O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB=90°.
又∵∠DAC=∠CAO,
∴△ADC∽△ACB,
∴
=
,即
=
.
∴AB=
,
∴sin∠CAB=sln∠DAC=
=
.
 (1)证明:连接OC.
(1)证明:连接OC.∵OC=OA,
∴∠CAO=∠OCA.
又∵AC平分∠DAB,
∴∠DAC=∠CAO,
∴∠DAC=∠CAO,
∴AD∥OC.
又∵直线CD与⊙O相切于点C,
∴∠OCD=90°,
∴∠ADC=90°,即AD⊥DC;
(2)解:连接BC.
由(1)知,∠ADC=90°,
∴根据勾股定理知,AC=
| AD2+CD2 |
∵AB为圆O的直径,
∴∠ACB=90°,
∴∠ADC=∠ACB=90°.
又∵∠DAC=∠CAO,
∴△ADC∽△ACB,
∴
| AD |
| AC |
| AC |
| AB |
| ||
| 3 |
| 3 |
| AB |
∴AB=
| 9 |
| 5 |
| 5 |
∴sin∠CAB=sln∠DAC=
| DC |
| AC |
| 2 |
| 3 |
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
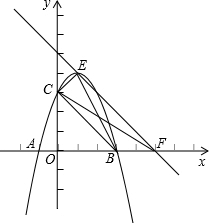 (2012•镇江二模)在平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0),与y轴的正半轴交于点C,顶点为E.
(2012•镇江二模)在平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)、B(3,0),与y轴的正半轴交于点C,顶点为E.