Question

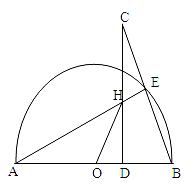
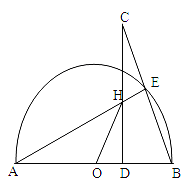
（本题12分）AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合。

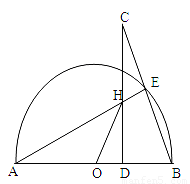
1.（1）求证：△AHD∽△CBD

2.（2）若CD=AB=2，求HD+HO的值。

 

Answer 1

【答案】

 

1.（1）证明：略………………4分

2.（2）设OD=x，则BD=1-x，AD=1+x

已证Rt△AHD∽Rt△CBD

   则HD : BD=AD : CD

   即HD : （1-x）=（1+x） : 2

     即HD=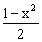………………………………3分

    在Rt△HOD中，由勾股定理得：

    OH==……………3分

所以HD+HO=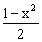+=1……………………………2分

【解析】略