题目内容
已知一次函数y1=ax+b的图象与反比例函数y2=| k | x |
 2,4)、(4,-2).
2,4)、(4,-2).(1)求两个函数的解析式;
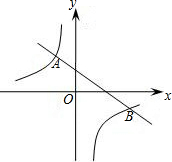
(2)结合图象写出y1<y2时,x的取值范围.
分析:(1)把坐标(-2,4)、(4,-2)分别代入一次函数y1=ax+b的图象与反比例函数y2=
即可求解.
(2)根据图象观察可直接得出答案.
| k |
| x |
(2)根据图象观察可直接得出答案.
解答:解:(1)把坐标(-2,4)、(4,-2)分别代入一次函数y1=ax+b,
∴
,解得:a=-1,b=2,∴y1=-x+2,
把坐标(-2,4)代入y2=
,解得:k=-8,
∴y2=
.
(2)根据图象观察知:当-2<x<0和x>4时,y1<y2成立.
故x的取值范围是:-2<x<0和x>4.
∴
|
把坐标(-2,4)代入y2=
| k |
| x |
∴y2=
| -8 |
| x |
(2)根据图象观察知:当-2<x<0和x>4时,y1<y2成立.
故x的取值范围是:-2<x<0和x>4.
点评:本题考查了反比例函数与一次函数的交点及用待定系数法求函数待定解析式,属于基础题,同学们要熟练掌握.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 (2012•德阳)已知一次函数y1=x+m的图象与反比例函数
(2012•德阳)已知一次函数y1=x+m的图象与反比例函数 已知一次函数y1=ax+b的图象与反比例函数y2=
已知一次函数y1=ax+b的图象与反比例函数y2= 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )