题目内容
如图,Rt△AOC中,∠ACO=90°,∠AOC=30°.将Rt△AOC绕OC中点E按顺时针方向旋转180°后得到Rt△BCO,BO、CO恰好分别在y轴、x轴上.再将Rt△BCO沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.(1)填空:CE:ED=______,AB:AC=______
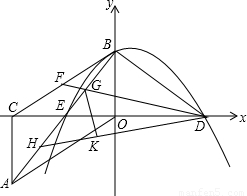
【答案】分析:(1)根据E是OC的中点,OD=OC即可求得CE:ED的值;在直角△AOC中,设AC=a,则OA=2a,OC=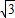 a,作AM⊥y轴,则在直角△ABM中,利用三角函数即可利用a表示得到AB的长,从而求得AB:AC的值;
a,作AM⊥y轴,则在直角△ABM中,利用三角函数即可利用a表示得到AB的长,从而求得AB:AC的值;
(2)易证△BDF∽△GBF∽△GDH,根据相似三角形的对应边的比相等,即可求得OD,OB的长度,即B、D的坐标,利用待定系数法即可求得函数的解析式;
(3)首先利用待定系数法求得抛物线的解析式,△BDQ的面积S可以表示成x的函数,然后根据函数的性质即可求得最值.
解答: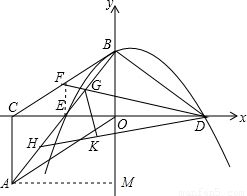 解:(1)在直角△AOC中,设AC=a,则OA=2a,OC=
解:(1)在直角△AOC中,设AC=a,则OA=2a,OC=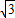 a,
a,
∵E是OC的中点,
∴OE=CE= OC,
OC,
又∵OD=OC
∴ED=3OE,
则CE:ED=3:1;
作AM⊥y轴,则AM=OC=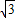 a,OM=AC=a,
a,OM=AC=a,
∴BM=OB+OM=2a,
在直角△ABM中,AB=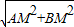 =
= =
= a,
a,
则AB:AC= :1;
:1;
(2)连接EF,
∵F是BC的中点,E是OC的中点,
∴EF= OB=
OB= AC=
AC= a,ED=
a,ED= a,∠FEO=90°
a,∠FEO=90°
在直角△EFD中,DF=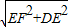 =
=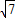 a,
a,
∴DF=AB,
又∵AC=BF,BC=BD
∴△ABC≌△FDB,
∴∠ABC=∠FDB,
又∵∠FBD=∠GFB
∴△BDF∽△GBF
∵∠GDH=∠FDB=∠CBA,
∠FGB=∠HGD
∴△GBF∽△GDH
设OB=2x,则BH=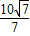 x
x
∴x=
∴BO=2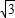 ,DO=6,
,DO=6,
∴y=-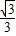 x+2
x+2
(3)OE= DO=3,则E的坐标是(-3,0),D的坐标是(6,0),B的坐标是(0,2
DO=3,则E的坐标是(-3,0),D的坐标是(6,0),B的坐标是(0,2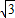 ),
),
设抛物线的解析式是:y=ax2+bx+c,
则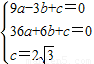 ,
,
解得: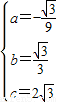
则抛物线解析式:y=-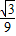 x2+
x2+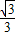 x+2
x+2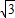
设△BDQ的面积为S,则S=- x2+
x2+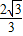 x
x
当x=3时,S取最大值,Q(3,2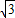 ).
).
点评:本题考查了二次函数的性质,待定系数法求解析式,以及全等三角形的判定与性质,二次函数的最值,是一个综合性较强的题目.
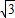 a,作AM⊥y轴,则在直角△ABM中,利用三角函数即可利用a表示得到AB的长,从而求得AB:AC的值;
a,作AM⊥y轴,则在直角△ABM中,利用三角函数即可利用a表示得到AB的长,从而求得AB:AC的值;(2)易证△BDF∽△GBF∽△GDH,根据相似三角形的对应边的比相等,即可求得OD,OB的长度,即B、D的坐标,利用待定系数法即可求得函数的解析式;
(3)首先利用待定系数法求得抛物线的解析式,△BDQ的面积S可以表示成x的函数,然后根据函数的性质即可求得最值.
解答:
 解:(1)在直角△AOC中,设AC=a,则OA=2a,OC=
解:(1)在直角△AOC中,设AC=a,则OA=2a,OC=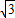 a,
a,∵E是OC的中点,
∴OE=CE=
 OC,
OC,又∵OD=OC
∴ED=3OE,
则CE:ED=3:1;
作AM⊥y轴,则AM=OC=
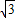 a,OM=AC=a,
a,OM=AC=a,∴BM=OB+OM=2a,
在直角△ABM中,AB=
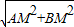 =
= =
= a,
a,则AB:AC=
 :1;
:1;(2)连接EF,
∵F是BC的中点,E是OC的中点,
∴EF=
 OB=
OB= AC=
AC= a,ED=
a,ED= a,∠FEO=90°
a,∠FEO=90°在直角△EFD中,DF=
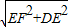 =
=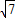 a,
a,∴DF=AB,
又∵AC=BF,BC=BD
∴△ABC≌△FDB,
∴∠ABC=∠FDB,
又∵∠FBD=∠GFB
∴△BDF∽△GBF
∵∠GDH=∠FDB=∠CBA,
∠FGB=∠HGD
∴△GBF∽△GDH
设OB=2x,则BH=
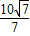 x
x∴x=

∴BO=2
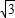 ,DO=6,
,DO=6,∴y=-
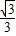 x+2
x+2
(3)OE=
 DO=3,则E的坐标是(-3,0),D的坐标是(6,0),B的坐标是(0,2
DO=3,则E的坐标是(-3,0),D的坐标是(6,0),B的坐标是(0,2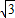 ),
),设抛物线的解析式是:y=ax2+bx+c,
则
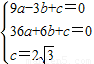 ,
,解得:
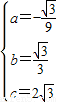
则抛物线解析式:y=-
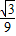 x2+
x2+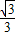 x+2
x+2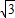
设△BDQ的面积为S,则S=-
 x2+
x2+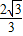 x
x 当x=3时,S取最大值,Q(3,2
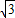 ).
).点评:本题考查了二次函数的性质,待定系数法求解析式,以及全等三角形的判定与性质,二次函数的最值,是一个综合性较强的题目.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
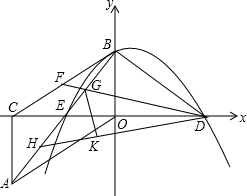 O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.
O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.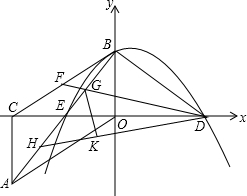 O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.
O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.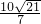 ,求直线BD解析式;
,求直线BD解析式;
 ,求直线BD解析式
,求直线BD解析式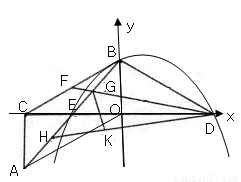
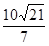 ,求直线BD解析式
,求直线BD解析式