题目内容
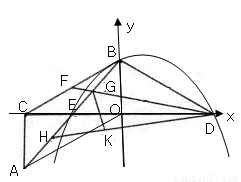
如图,Rt△AOC中,∠ACO=90°,∠AOC=30°.将Rt△AOC绕OC中点E按顺时针方向旋转180°后得到Rt△BCO,BO、CO恰好分别在y轴、x轴上.再将Rt△BCO沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.
【小题1】填空:CE:ED=________,AB:AC=__________;
【小题2】若BH=
 ,求直线BD解析式
,求直线BD解析式【小题3】在(2)的条件下,一抛物线过点D、点E、点B,此抛物线位于直线BD上方有一动点Q,△BDQ的面积有无最大值?若有,请求出点Q的坐标;若无,请说明理由
【小题1】见解析
【小题2】
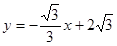
【小题3】当x=3时,S取最大值,Q(3,
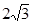 )解析:
)解析:(1)1:3,
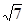 :1
:1 (2)易证△BDF∽△GBF∽△GDH,
设OB=2x,则BH=
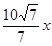 ∴x=
∴x=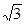
∴BO=2
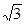 ,DO=6,
,DO=6,∴
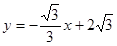
(3)抛物线解析式:
 ,
, 设△BDQ的面积为S,则S=
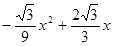
当x=3时,S取最大值,Q(3,
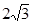 )
) 
练习册系列答案
相关题目
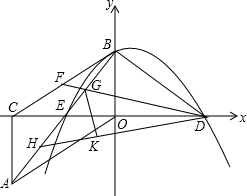 O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.
O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.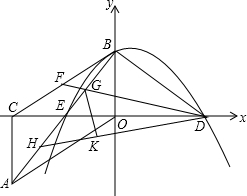 O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.
O沿y轴对折得到Rt△BDO.取BC中点F,连接DF,交AB于点G,将△BDG沿DF对折得到△KDG.直线DK交AB于点H.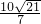 ,求直线BD解析式;
,求直线BD解析式;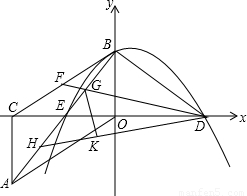
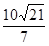 ,求直线BD解析式
,求直线BD解析式