Question

【题目】如图，△ABC中，∠ACB=90°，D为AB上任一点，过D作AB的垂线，分别交边AC、BC的延长线于E、F两点，∠BAC、∠BFD的平分线交于点I，AI交DF于点M，FI交AC于点N，连接BI．下列结论：①∠BAC=∠BFD；②∠ENI=∠EMI；③AI⊥FI；④∠ABI=∠FBI；其中正确结论的个数是（ ）

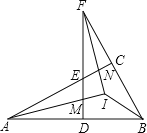
A．1个 B．2个 C．3个 D．4个

Answer 1

【答案】C

【解析】

试题分析：先根据∠ACB=90°可知∠DBF+∠BAC=90°，再由FD⊥AB可知∠BDF=90°，所以∠DBF+∠BFD=90°，通过等量代换即可得出∠BAC=∠BFD，故①正确；根据∠BAC=∠BFD，∠BAC、∠BFD的平分线交于点I可知∠EFN=∠EAM，再由对顶角相等可知∠FEN=∠AEM，根据三角形外角的性质即可判断出∠ENI=∠EMI，故②正确；由①知∠BAC=∠BFD，因为∠BAC、∠BFD的平分线交于点I，故∠MAD=∠MFI，再根据∠AMD=∠FMI可知，∠AIF=∠ADM=90°，即AI⊥FI，故③正确；因为BI不是∠B的平分线，所以∠ABI≠∠FBI，故④错误．

解：∵∠ACB=90°，

∴∠DBF+∠BAC=90°，

∵FD⊥AB，

∴∠BDF=90°，

∴∠DBF+∠BFD=90°，

∴∠BAC=∠BFD，故①正确；

∵∠BAC=∠BFD，∠BAC、∠BFD的平分线交于点I，

∴∠EFN=∠EAM，

∵∠FEN=∠AEM，

∴∠ENI=∠EMI，故②正确；

∵由①知∠BAC=∠BFD，∠BAC、∠BFD的平分线交于点I，

∴∠MAD=∠MFI，

∵∠AMD=∠FMI，

∴∠AIF=∠ADM=90°，即AI⊥FI，故③正确；

∵BI不是∠B的平分线，

∴∠ABI≠∠FBI，故④错误．

故选C．