题目内容
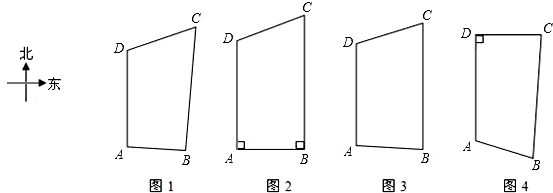
佛山市的名片----“一环”路全长约为99公里,其中:东线长36公里,西线长32公里,南线长15公里,北线长15.6公里(为计算方便,以上数据与实际稍有出入)小明同学想根据以上信息估算“一环”路的环内面积,他把佛山“一环”路的形状理想化为一个四边形进行研究,他想到的图形有如下四种:

(1)如果让你来研究,你会选择哪个图形?(注:图3中AD∥BC)
请你利用选定的图形,把所给信息中的三个数据作为其中三边的长,计算出第四边的长,并比较它与实际长的误差是多少?
参考数据:
 =15.53,
=15.53, =14.46,
=14.46, =15.08,
=15.08, =4.28.
=4.28.(2)假设边长的误差在0.5公里以内,就可以用所选择的图形近似计算环内面积.你选择的图形是否符合以上?假设若符合,请计算出环内面积.

【答案】分析:本题是一个直角梯形,过点D作DE⊥BC,在直角△CDE中根据三角函数就可以求解.
解答: 解:(1)选择图2,三边长分别为AD=32,AB=15,BC=36(3分)
解:(1)选择图2,三边长分别为AD=32,AB=15,BC=36(3分)
过D点作DE⊥CB于E,则四边形ABED是矩形(4分)
∴DE=AB=15,BE=AD=32
∴EC=4(5分)
在Rt△CDE中, (6分)
(6分)
∴15.6-15.53=0.07
∴与北线长度相比,误差是0.07公里;(7分)
(2)由(1)可知,可以把“一环”近似的看作图2,其面积为 ;
;
答:“一环”的环内面积大约是510平方公里.(10分)
(注:若选三边为AB、AD、CD,则求得BC=36.28,面积约为512平方公里;若选三边为AB、BC、CD,则求得AD=31.72,面积约为508平方公里.若选图形1,则认为不能做;若图形3、4,视解答情况酌情给分)
点评:直角梯形的问题可以通过作高线转化为解直角三角形的问题来解决.
解答:
 解:(1)选择图2,三边长分别为AD=32,AB=15,BC=36(3分)
解:(1)选择图2,三边长分别为AD=32,AB=15,BC=36(3分)过D点作DE⊥CB于E,则四边形ABED是矩形(4分)
∴DE=AB=15,BE=AD=32
∴EC=4(5分)
在Rt△CDE中,
 (6分)
(6分)∴15.6-15.53=0.07
∴与北线长度相比,误差是0.07公里;(7分)
(2)由(1)可知,可以把“一环”近似的看作图2,其面积为
 ;
;答:“一环”的环内面积大约是510平方公里.(10分)
(注:若选三边为AB、AD、CD,则求得BC=36.28,面积约为512平方公里;若选三边为AB、BC、CD,则求得AD=31.72,面积约为508平方公里.若选图形1,则认为不能做;若图形3、4,视解答情况酌情给分)
点评:直角梯形的问题可以通过作高线转化为解直角三角形的问题来解决.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目

 =15.53,
=15.53, =14.46,
=14.46, =15.08,
=15.08, =4.28.
=4.28.
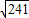 =15.53,
=15.53, =14.46,
=14.46, =15.08,
=15.08, =4.28.
=4.28.

 =15.53,
=15.53,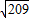 =14.46,
=14.46,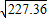 =15.08,
=15.08, =4.28.
=4.28.