��Ŀ����
����Ŀ����ͼ���ڵ���ֱ��������ABC�У���BAC=90�㣬AC=8 ![]() cm��AD��BC�ڵ�D����P�ӵ�A��������A��C������
cm��AD��BC�ڵ�D����P�ӵ�A��������A��C������ ![]() cm/s���ٶ��˶�����Cֹͣ�����˶������У�����P��PQ��AB��BC�ڵ�Q�����߶�PQΪ��������ֱ��������PQM���ҡ�PQM=90�㣨��M��Cλ��PQ��ࣩ�����P���˶�ʱ��Ϊx��s������PQM���ADC�ص����ֵ����Ϊy��cm2��
cm/s���ٶ��˶�����Cֹͣ�����˶������У�����P��PQ��AB��BC�ڵ�Q�����߶�PQΪ��������ֱ��������PQM���ҡ�PQM=90�㣨��M��Cλ��PQ��ࣩ�����P���˶�ʱ��Ϊx��s������PQM���ADC�ص����ֵ����Ϊy��cm2��
��1������M����AB��ʱ��x=��
��2������M����AD��ʱ��x=��
��3����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
���𰸡�
��1��4
��2��![]()
��3��
�⣺�ٵ�0��x��4ʱ����ͼ2�У���PM��PQ�ֱ�AD�ڵ�E��F�����ص�����Ϊ��PEF��
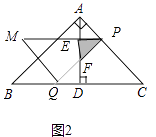
��AP= ![]() x��
x��
��EF=PE=x��
��y=S��PEF= ![]() PEEF=
PEEF= ![]() x2��
x2��
�ڵ�4��x�� ![]() ʱ����ͼ3�У���PM��MQ�ֱ�AD��E��G�����ص�����Ϊ�ı���PEGQ��
ʱ����ͼ3�У���PM��MQ�ֱ�AD��E��G�����ص�����Ϊ�ı���PEGQ��
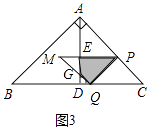
��PQ=PC=8 ![]() ��
�� ![]() x��
x��
��PM=16��2x����ME=PM��PE=16��3x��
��y=S��PMQ��S��MEG= ![]() ��8
��8 ![]() ��
�� ![]() x��2��
x��2�� ![]() ��16��3x��2=��
��16��3x��2=�� ![]() x2+32x��64��
x2+32x��64��
�۵� ![]() ��x��8ʱ����ͼ4�У����غϲ���Ϊ��PMQ��
��x��8ʱ����ͼ4�У����غϲ���Ϊ��PMQ��
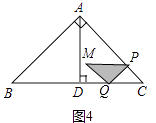
��y=S��PMQ= ![]() PQ2=
PQ2= ![]() ��8
��8 ![]() ��
�� ![]() x��2=x2��16x+64��
x��2=x2��16x+64��
��������y= 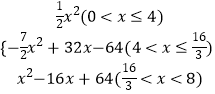
���������⣺��1������M����AB��ʱ���ı���AMQP�������Σ���ʱ��D���Q�غϣ�AP=CP=4 ![]() ������x=
������x= ![]() =4��
=4��
���Դ���4����2����ͼ1�У�����M����AD��ʱ����PE��QC��E��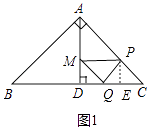 br />�ߡ�MQP����PQE����PEC���ǵ���ֱ�������Σ�MQ=PQ=PC
br />�ߡ�MQP����PQE����PEC���ǵ���ֱ�������Σ�MQ=PQ=PC
��DQ=QE=EC��
��PE��AD��
�� ![]() =
= ![]() =
= ![]() ����AC=8
����AC=8 ![]() ��
��
��PA= ![]() ��
��
��x= ![]() ��
�� ![]() =
= ![]() ��
��
���Դ��� ![]() ��
��





