题目内容
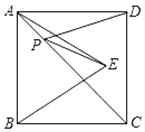
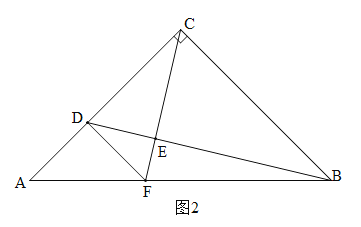
【题目】如图,△ABC中,∠ACB=90°,AC=BC,D是AC边上一点,AD=nCD,CE⊥BD于E交AB于F,连接DF.
(1)如图,当BF=2AF时,求证:n=1;
(2)如图,当DF//BC时,求![]() 的值.
的值.

【答案】(1)n=1;(2)![]()
【解析】分析:(1)作AG∥BC交CF延长线于G,则![]() ,可证明△ACG≌△CBD ,得到AG=CD .
,可证明△ACG≌△CBD ,得到AG=CD .
由AC=BC,得到AG:BC=CD:AC=![]() ,即可得到结论.
,即可得到结论.
(2)由DF∥BC,得到∠CDF=∠BCD=90°.再由∠DCE=∠EBE,得到△CDF∽△BCD,由相似三角形的性质得到DF:DC=CD:BC.可证明AD=DF.令CD=1,则DF=AD=n,BC=AC=n+1, 得到n:1=1:(n+1),解方程得到n的值.再证明△DEF∽△CDF,得到DE:EF=CD:DF=![]() ,即可得到结论.
,即可得到结论.
详解:(1)如图1,作AG∥BC交CF延长线于G,则![]() .
.
∵∠ACB=90°,∴∠ACF+∠ECB=90°.
∵CE⊥BD,∴∠ECB+∠CBE=90°,∴∠ACE=∠CBE.
∵AG∥BC,∠ACB=90°,∴∠GAC=180°-90°=90°,∴∠GAC=∠DCB.
在△ACG和△CBD中,∵∠∠GAC=∠DCB,AC=CB,∠ACE=∠CBE,∴△ACG≌△CBD ,∴AG=CD .
∵AC=BC,∴AG:BC=CD:AC=![]() ,∴AC=2CD,∴AD=CD.
,∴AC=2CD,∴AD=CD.
∵AD=nCD,∴n=1.
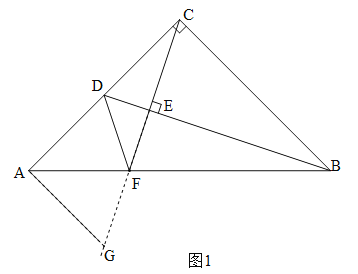
(2)如图2.
∵DF∥BC,∠ACB=90°,∴∠CDF=180°-90°=90°,∴∠CDF=∠BCD=90°.
∵∠DCE=∠EBE,∴△CDF∽△BCD,∴DF:DC=CD:BC.
∵AC=CB,∠ACB=90°,∴∠A=45°.
∵∠CDF=90°,∴∠ADF=90°,∴∠DFA=45°,∴AD=DF.令CD=1,则DF=AD=n,BC=AC=n+1, ∴n:1=1:(n+1),∴n=![]() (负数舍去),∴n=
(负数舍去),∴n=![]() .
.
∵CE⊥BD,∴∠DEF=90°.
∵∠CDF=90°,∴∠DEF=∠CDF=90°.
∵∠DFE=∠DFE,∴△DEF∽△CDF,∴DE:EF=CD:DF=![]() =
=![]() .
.

【题目】某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩![]() 及其方差S2如表所示:
及其方差S2如表所示:
甲 | 乙 | 丙 | 丁 | |
(环) | 8.4 | 8.6 | 8.6 | 7.6 |
S2 | 0.74 | 0.56 | 0.94 | 1.92 |
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁