题目内容
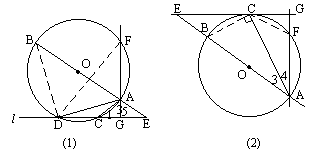
(1)如图中，已知直线AB过圆心O，交⊙O于A，B，直线AF交⊙O于F(不与B重合)，直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连结AC，AD．
求证：(1)①∠BAD＝∠CAG；②AC·AD＝AE·AF．(2)在问题(1)中，直线l向上平移，使l与⊙O相切，其他条件不变．
①请你在图中标记字母(重合点任选其中一个字母标记)；②新图形中，相应于问题(1)中的两个结论(相应字母随新字母变更)是否成立？如果成立，请给出证明：如果不成立；请说明理由．
解析：
|
解答：(1)①连BD，由AB是⊙O直径，得∠ADB＝
②连DF，由四边形ACDF内接于⊙O，得∠1＝∠AFD，又∠2＝∠3，∠4＝∠5，∴∠2＋∠4＝∠3＋∠5，而△ACE∽△AFD，∴ (2)当直线l向上平移与⊙O相切于C点，(1)中两个结论改为：①∠BAC＝∠CAG，②AC2＝AE·AF，这两个结论仍成立，证明如下： ①连结CB，CG切⊙O于C，得∠1＝∠2，AB是⊙O直径，得∠2＋∠3＝ ②连结CF，由∠GCA＝∠2＝∠GFC，得∠ECA＝∠CFA． 再由∠3＝∠4，可得△AFC∽△ACE，从而得AC2＝AE·AF，(如图) |
，∴∠2＋∠B＝
，又∵四边形ABCD内接于⊙O，∴∠1＝∠B，AF⊥l于G，∴∠1＋∠3＝
，∴∠2＝∠3，(如图(2))即∠BAD＝∠CAG．
＝
，即AC·AD＝AF·AE．
，CG⊥AG，得∠1＋∠4＝
，即∠3＝∠4，则∠BAC＝∠CAG．提示：
|
名师导引：(1)综合运用圆周角，圆内接四边形，直径所对圆周角为 探究点：(2)是否成立，正确画出图形①从切线相关性质，圆周角，圆内接四边形有关角的特征分析，得出∠2＋∠3＝ |
，三角形相似识别定理加以分析．①∠1＝∠B，∠2＋∠B＝
，这是关键等量关系，②∠2＋∠4＝∠3＋∠5可推出(如图(1))△ACE∽△AFD，(2)画图探究仍然成立．
，∠1＋∠4＝
，②探索△AFC∽△ACE，关键证∠ECA＝∠CFA．
阅读快车系列答案
