题目内容
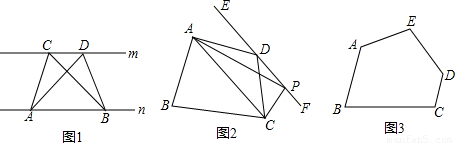
(1)如图1,已知直线m∥n,A,B为直线n上的两点,C,D为直线m上的两点.①请你判断△ABC与△ABD的面积具有怎样的关系?
②若点D在直线m上可以任意移动,△ABD的面积是否发生变化?并说明你的理由.
(2)如图2,已知:在四边形ABCD中,连接AC,过点D作EF∥AC,P为EF上任意一点(与点D不重合).请你说明四边形ABCD的面积与四边形ABCP的面积相等.
(3)如图3是一块五边形花坛的示意图.为了使其更规整一些,园林管理人员准备将其修整为四边形,根据花坛周边的情况,计划在BC的延长线上取一点F,沿EF取直,构成新的四边形ABFE,并使得四边形ABFE的面积与五边形ABCDE的面积相等.请你在图3中画出符合要求的四边形ABFE,并说明理由.
【答案】分析:(1)两条平行线间的距离一定,那么△ABC与△ABD同底等高,所以面积相等;
(2)由(1)得△DCA和△PAC的面积相等,那么都加上△ABC的面积也相等,即四边形ABCD的面积与四边形ABCP的面积相等;
(3)只需把△EDC转移即可,那么应仿照(2)的做法,应连接EC,过点D作平行线,构造和△EDC等底同高的三角形.
解答:解:(1)①S△ABC=S△ABD;(1分)
②△ABD的面积不发生变化.因为不论点D在直线m上移动到哪一位置,点D到直线n的距离都不变,所以△ABD的面积不变.(3分)
(2)因为EF∥AC,所以点D,P到直线AC的距离相等,所以△ACD的面积与△ACP的面积相等.所以四边形ABCD的面积与四边形ABCP的面积相等.(6分)
(3)连接CE,过点D作DF∥CE,交BC的延长线于点F,连接EF,四边形ABFE就是符合要求的四边形.如图1所示.(8分)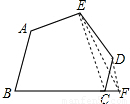
因为DF∥EC,所以点D,F到线段EC的距离相等,
所以△ECD的面积与△ECF的面积相等,所以四边形ABFE的面积与五边形ABCDE的面积相等.(10分)
点评:本题用到的知识点为:两条平行线间的距离是个定值;同底等高的三角形的面积相等.
(2)由(1)得△DCA和△PAC的面积相等,那么都加上△ABC的面积也相等,即四边形ABCD的面积与四边形ABCP的面积相等;
(3)只需把△EDC转移即可,那么应仿照(2)的做法,应连接EC,过点D作平行线,构造和△EDC等底同高的三角形.
解答:解:(1)①S△ABC=S△ABD;(1分)
②△ABD的面积不发生变化.因为不论点D在直线m上移动到哪一位置,点D到直线n的距离都不变,所以△ABD的面积不变.(3分)
(2)因为EF∥AC,所以点D,P到直线AC的距离相等,所以△ACD的面积与△ACP的面积相等.所以四边形ABCD的面积与四边形ABCP的面积相等.(6分)
(3)连接CE,过点D作DF∥CE,交BC的延长线于点F,连接EF,四边形ABFE就是符合要求的四边形.如图1所示.(8分)

因为DF∥EC,所以点D,F到线段EC的距离相等,
所以△ECD的面积与△ECF的面积相等,所以四边形ABFE的面积与五边形ABCDE的面积相等.(10分)
点评:本题用到的知识点为:两条平行线间的距离是个定值;同底等高的三角形的面积相等.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目

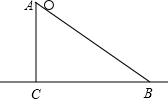 在地面上有一个斜坡装置(如图),已知斜坡的铅直高度AC=0.6m,水平距离BC=0.8m,小球从顶端A由静止自由下滑,速度均匀增大,0.2s滑至底端B后,继续在平地上滑行15米停止.
在地面上有一个斜坡装置(如图),已知斜坡的铅直高度AC=0.6m,水平距离BC=0.8m,小球从顶端A由静止自由下滑,速度均匀增大,0.2s滑至底端B后,继续在平地上滑行15米停止.

