题目内容
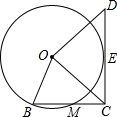 如图,四边形OBCD中,∠BCD=90°,E为CD的中点,以OB为半径的⊙O切CD于E,交BC于M,若BM=CM=2,则OC的长为( )
如图,四边形OBCD中,∠BCD=90°,E为CD的中点,以OB为半径的⊙O切CD于E,交BC于M,若BM=CM=2,则OC的长为( )A、4
| ||
| B、3 | ||
C、
| ||
D、
|
考点:切线的性质
专题:
分析:连接OM、OE,过O作OF⊥BC于F,根据垂径定理求出BF=FM=1,求出CF=3,证四边形OFCE是矩形,得出OE=CF=OB=3,CE=OF,根据勾股定理求出OF,根据勾股定理求出OC即可.
解答:解: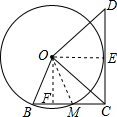
连接OM、OE,过O作OF⊥BC于F,
∵OF过O,
∴BF=FM=1,
∴FC=1+2=3,
∵DC切⊙O于E,∠BCD=90°,OF⊥BC,
∴∠OEC=∠ECF=∠OFC=90°,
∴四边形OFCE是矩形,
∴OE=FC=3,CE=OF,
∴OB=OE=3,
在Rt△OFB中,OB=3,BF=1,由勾股定理得:OF=2
=CE,
在Rt△OFC中,OF=2
,CF=3,由勾股定理得:OC=
=
,
故选C.

连接OM、OE,过O作OF⊥BC于F,
∵OF过O,
∴BF=FM=1,
∴FC=1+2=3,
∵DC切⊙O于E,∠BCD=90°,OF⊥BC,
∴∠OEC=∠ECF=∠OFC=90°,
∴四边形OFCE是矩形,
∴OE=FC=3,CE=OF,
∴OB=OE=3,
在Rt△OFB中,OB=3,BF=1,由勾股定理得:OF=2
| 2 |
在Rt△OFC中,OF=2
| 2 |
(2
|
| 17 |
故选C.
点评:本题考查了矩形的性质和判定,勾股定理,垂径定理,切线的性质的应用,关键是求出CF、OF的长和构造直角三角形.

练习册系列答案
相关题目
下列各题中,分解因式错误的是( )
| A、x2-1=(x+1)(x-1) |
| B、(-2y)2-x2=(-2y+x)(2y-x) |
| C、81x2-64y2=(9x+8y)(9x-8y) |
| D、1-4y2=(1+2y)(1-2y) |
下列运算正确的是( )
| A、m-2(n-7)=m-2n-14 | ||||
B、-
| ||||
| C、2x+(-3x)=5x | ||||
| D、x-y+z=x-(y-z) |
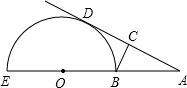 如图,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,sin∠A=
如图,EB为半圆O的直径,点A在EB的延长线上,AD切半圆O于点D,BC⊥AD于点C,sin∠A= 如图,△ABC中,∠A=30°,∠C=90°,AC=4cm,以C为圆心,2cm为半径作⊙C,则直线AB与已知⊙C的位置关系是
如图,△ABC中,∠A=30°,∠C=90°,AC=4cm,以C为圆心,2cm为半径作⊙C,则直线AB与已知⊙C的位置关系是
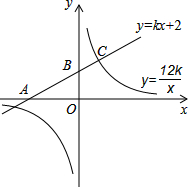 已知反比例函数y=
已知反比例函数y= 如图,△ABC边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,则PM的值是
如图,△ABC边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,则PM的值是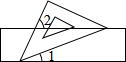 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=15°,则∠2的度数是
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.若∠1=15°,则∠2的度数是