题目内容
【题目】观察下列等式:
(x-1)(x+1)= x2 -1,
(x-1)(x2 +x+1)=x3 -1,
(x-1)(x3+x2 +x+1)=_________,………
(1)猜想规律(x-1)(xn +xn-1+…+x2 +x+1)=______,
(2)根据上面的结论,你能求出下面式子的结果吗?
(x20 -1)÷(x-1)=_______,
(3)已知x3+x2 +x+1=0,求x2012的值.
【答案】x4-1;(1)![]() ;(2)x 19 +x 18+…+x 2 +x+1;(3)x2012=1.
;(2)x 19 +x 18+…+x 2 +x+1;(3)x2012=1.
【解析】
(1)根据已知等式得到规律:等式的右边是两项,且x的指数比左边式子后边括号中x的最高指数大1;
(2)根据(1)的结论即可直接得到答案;
(3)由x 3+x 2 +x+1=0,得到(x-1)(x 3+x 2 +x+1)=0,即可得到x4-1=0,由此求得x2012=1.
x4-1,
(1)![]() ;
;
(2)(x20 -1)÷(x-1)=x 19 +x 18+…+x 2 +x+1;
(3)∵x 3+x 2 +x+1=0,
∴(x-1)(x 3+x 2 +x+1)=0,
∴x4-1=0,
∴x4=1,
∴x2012=1.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
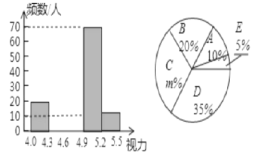
【题目】某市在今年对全市6000名八年级学生进行了一次视力抽样调查,并根据统计数据,制作了的统计表和如图所示统计图.
组别 | 视力 | 频数(人) |
A |
| 20 |
B |
| a |
C |
| b |
D |
| 70 |
E |
| 10 |
请根据图表信息回答下列问题:
(1)求抽样调查的人数;
(2)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(3)补全频数分布直方图;
(4)若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是多少?根据上述信息估计该市今年八年级的学生视力正常的学生大约有多少人?