Question

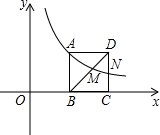（2007•中山区二模）如图，正方形ABCD的边BC在x轴的正半轴上，OB=1，M为对角线BD的中点，函数y=

3

x

的图象经过A、M两点，与CD交于点N，则CN：DN的值为

1：3

．

Answer 1

分析：先根据OB=1求出B点坐标，再由正方形的性质可知A点横坐标等于1，故可得出A点坐标，进而可得出正方形的边长，故可求出CD两点的坐标，再求出N点坐标即可得出CN及DN的长，故可得出结论．

解答：解：∵OB=1，
∴B（1，0），
∵四边形ABCD是正方形，
∴A点的横坐标为1，
∵函数y=

3

x

的图象经过A点，
∴当x=1时，y=3，
∴A（1，3），即正方形ABCD的边长等于3，
∴C（4，0），D（4，3），
∴直线CD的表达式为x=4，
∵点N是反比例函数y=

3

x

与直线x=4的交点，
∴N（4，

3

4

），
∴CN=

3

4

，DN=3-

3

4

=

9

4

，
∴CN：DN=

3

4

：

9

4

=1：3．
故答案为：1：3．

点评：本题考查的是反比例函数综合题及正方形的性质，熟知反比例函数图象上点的坐标特点及用待定系数法求函数的解析式是解答此题的关键．