题目内容
【题目】已知点I为△ABC的内心
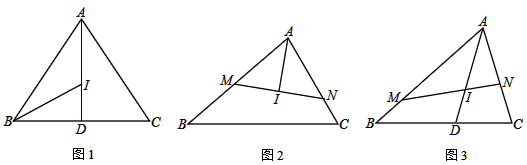
(1) 如图1,AI交BC于点D,若AB=AC=6,BC=4,求AI的长
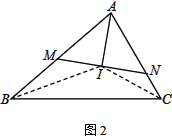
(2) 如图2,过点I作直线交AB于点M,交AC于点N
① 若MN⊥AI,求证:MI2=BM·CN
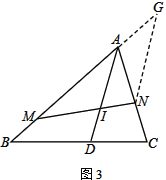
② 如图3,AI交BC于点D.若∠BAC=60°,AI=4,请直接写出![]() 的值
的值
【答案】(1)AI的长是![]() ;
;
(2)①证明见解析;② ![]()
【解析】试题分析:(1)、根据内心的性质得出AD为线段BC的中垂线,然后根据Rt△BID的勾股定理得出答案;(2)、首先得出△AMI和△ANI全等,从而得出∠AMN=∠ANM,然后连接BI和CI,根据角度之间的关系得出△BMI和△INC相似,则NI2=BM·CN,根据NI=MI得出答案;(3)、过点N作NG∥AD交MA的延长线于G,则∠ANG=∠AGN=30° ∴AN=AG,NG=![]() 然后根据平行线性质得出
然后根据平行线性质得出![]() ,然后代入得出答案.
,然后代入得出答案.
试题解析:(1) ![]()
(2) ∵I为△ABC的内心 AI⊥MN ∴△AMI≌△ANI(ASA) ∴∠AMN=∠ANM
连接BI、CI ∴∠BMI=∠CNI
设∠BAI=∠CAI=α,∠ACI=∠BCI=β ∴∠NIC=90°-α-β
∵∠ABC=180°-2α-2β ∴∠MBI=90°-α-β ∴△BMI∽△INC
∴![]() ∴NI2=BM·CN ∵NI=MI ∴MI2=BM·CN
∴NI2=BM·CN ∵NI=MI ∴MI2=BM·CN
(3) 过点N作NG∥AD交MA的延长线于G ∴∠ANG=∠AGN=30° ∴AN=AG,NG=![]()
∵AI∥NG ∴![]() ∴
∴![]() ,得
,得![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目