题目内容
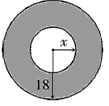
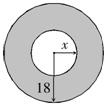 18、如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.
18、如图,在一个半径为18cm的圆面上,从中心挖去一个小圆面,当挖去小圆的半径由小变大时,剩下的一个圆环面积也随之发生变化.(1)在这个变化过程中,自变量、因变量各是什么?
(2)如挖去的圆半径为x(cm),圆环的面积y(cm2)与x的关系式是
y=324π-πx2
;(3)当挖去圆的半径由1cm变化到9cm时,圆环面的面积由
323π
cm2变化到243π
cm2.分析:(1)在函数中,给一个变量x一个值,另一个变量y就有对应的值,则x是自变量,y是因变量,据此即可判断;
(2)圆环的面积就是大圆的面积与挖去的小圆的面积的差;
(3)在函数解析式中分别求出半径x,分别是1cm与9cm时,面积的值,即可求解.
(2)圆环的面积就是大圆的面积与挖去的小圆的面积的差;
(3)在函数解析式中分别求出半径x,分别是1cm与9cm时,面积的值,即可求解.
解答:解:(1)自变量很小圆的半径,因变量是圆环的面积;
(2)y=324π-πx2;
(3)在y=324π-πx2中,当x=1时,y=323π;
当x=9时,y=243π.故圆环面的面积由323πcm2变化到243πcm2.
(2)y=324π-πx2;
(3)在y=324π-πx2中,当x=1时,y=323π;
当x=9时,y=243π.故圆环面的面积由323πcm2变化到243πcm2.
点评:正确理解自变量与因变量的定义,圆环的面积等于大圆面积与小圆面积的差是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
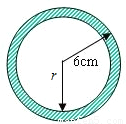
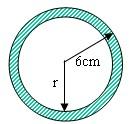 3、如图,在一个半径为6cm圆形纸片上,挖去一个半径为r cm的圆,若余下圆环面积为11π,则r为( )
3、如图,在一个半径为6cm圆形纸片上,挖去一个半径为r cm的圆,若余下圆环面积为11π,则r为( ) 如图,在一个半径为1cm的圆形铁皮上剪下一个角为60°的阴影BAC,用它围成一个圆锥的侧面,则圆锥的底面圆的半径为
如图,在一个半径为1cm的圆形铁皮上剪下一个角为60°的阴影BAC,用它围成一个圆锥的侧面,则圆锥的底面圆的半径为