��Ŀ����
����Ŀ���������龳��
����ʦ������ѧϰ��С����С���������һ�����⣺
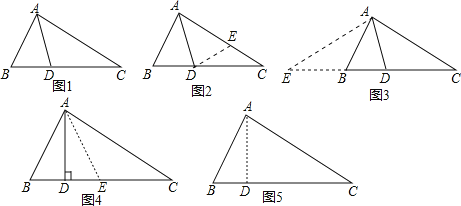
��ͼ1����ABC�У���B=2��C��AD����BAC��ƽ���ߣ���֤��AB+BD=AC
С����֤��˼·�ǣ���AC�Ͻ�ȡAE=AB������DE������ͼ2����
С�ݵ�֤��˼·�ǣ��ӳ�CB����E��ʹBE=AB������AE�� ����֤�ã�AE=DE����ͼ3����
��������ѡ��һ��˼·���������һ����֤����
����ʽ̽����
��AD����BAC��ƽ�������ij���AD��BC���ϵĸ����������������䣮����ͼ4����AB+BD=AC����������������֤��������������д�������ȷ���ۣ���˵�����ɣ�
��Ǩ����չ��
��ABC�У���B=2��C�� ��֤��AC2=AB2+ABBC�� ����ͼ5��

���𰸡�������
��������
���������龳��С����֤��˼·�ǣ���AC�Ͻ�ȡAE=AB���ɽ�ƽ���ߵ����ʾͿ��Եó���DAB=��DAE����֤����ADB��ADE�Ϳ��Եó����ۣ�С�ݵ�֤��˼·�ǣ��ӳ�CB����E��ʹBE=AB������AE���Ϳ��Եó���E=��C������AE=AC�������ó�AE=ED���ɣ�
��ʽ̽����CD�Ͻ�ȡDE=DB������AE����AD��BC�Ϳ��Եó�AE=AB����AED=��B������AED=��C+��CAE������C=��CAE�ó�AE=EC�������ó����ۣ�
Ǩ����չ������A��AD��BC��D���ɹ��ɶ����ã�AB2=BD2+AD2��AC2=CD2+AD2��AC2��AB2=CD2��BD2=BC��CD��BD�����ɣ�2���Ľ��۾Ϳ��Եó�AC2��AB2=BC��CD��BD��=BCAB���ɣ�
�⣺�����龳��С����֤��˼·�ǣ���ͼ2����AC�Ͻ�ȡAE=AB������DE������ͼ2��
��AD����BAC��ƽ���ߣ�
���BAD=��EAD��
����ABD����AED��
 ��
��
���ABD�ա�AED��SAS����
��BD=DE����ABD=��AED
�ߡ�AED=��EDC+��C����B=2��C��
���EDC=��C��
��DE=EC��
��AB+BD=AC��
С�ݵ�֤��˼·�ǣ���ͼ3���ӳ�CB����E��ʹBE=AB������AE��
���E=��BAE��
�ߡ�ABC=��E+��BAE��
���ABC=2��E��
�ߡ�ABC=2��C��
���E=��C��
���AEC�ǵ��������Σ�
��AD����BAC��ƽ���ߣ�
���BAD=��DAC��
�ߡ�ADE=��DAC+��C����DAE=��BAD+��BAE
���ADE=��DAE��
��EA=ED=AC��
��AB+BD=AC��
��ʽ̽����
AB+BD=AC������ ��ȷ���ۣ�AB+BD=CD����5�֣�
���ɣ���ͼ4����CD�Ͻ�ȡDE=DB������AE��
��AD��BC��
��AD��BE���д��ߣ�
��AE=AB��
���B=��AED��
�ߡ�AED=��C+��CAE������B=2��C��
���C=��CAE��
��AE=EC��
��AB+BD=CD��
Ǩ����չ��
֤������ͼ5������A��AD��BC��D���ɹ��ɶ����ã�AB2=BD2+AD2��AC2=CD2+AD2��
��AC2��AB2=CD2��BD2=��CD+BD����CD��BD��=BC��CD��BD��
��AB+BD=CD��
��CD��BD=AB��
��AC2��AB2=BC��CD��BD��=BCAB��
��AC2=AB2+ABBC��

 ��У����ϵ�д�
��У����ϵ�д�




