题目内容
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点E,连接OE、AE,过点E作⊙O的切线交边BC于F.

(1)求证:△ODE∽△ECF;
(2)在点O的运动过程中,设DE= ![]() :
:
①求![]() 的最大值,并求此时⊙O的半径长;
的最大值,并求此时⊙O的半径长;
②判断△CEF的周长是否为定值,若是,求出△CEF的周长;否则,请说明理由?
【答案】(1)证明见解析;(2)①5;②16.
【解析】试题分析:(1)根据∠OEF=90°得出∠OED+∠CEF=90°,根据∠CEF+∠CFE=90°得出∠OED=∠EFC,最后根据∠D=∠C即可证出△ODE∽△ECF;
(2)①根据△ODE∽△ECF,得出ODCF=DEEC,设DE=x,得出ODCF=-(x-4)2+16,从而求出最大值,设此时半径为r,根据OD2+DE2=OE2,得出(8-r)2+42=r2,解方程即可;
②在Rt△ODE中,根据OD2+DE2=OE2,OA=OE,得出(8-OE)2+x2=OE2,求出OE=4+![]() ,OD=4-
,OD=4-![]() ,根据Rt△DOE∽Rt△CEF,得出
,根据Rt△DOE∽Rt△CEF,得出![]() ,代入得出CF=
,代入得出CF=![]() ,EF=
,EF=![]() ,最后根据△CEF的周长=CE+CF+EF代入计算即可得出△CEF的周长=16,是定值.
,最后根据△CEF的周长=CE+CF+EF代入计算即可得出△CEF的周长=16,是定值.
试题解析:(1)证明:∵EF切⊙O于点M,
∴∠OEF=90°,
∴∠OED+∠CEF=90°,
∵∠C=90°,
∴∠CEF+∠CFE=90°,
∴∠OED=∠EFC,
∵∠D=∠C=90°,
∴△ODE∽△ECF;
(2)解:①由(1)知:△ODE∽△ECF,
∴![]() ,
,
∴ODCF=DEEC,
∵DE=x,
∴EC=8-x,
∴ODCF=x(8-x)=-x2+8x=-(x-4)2+16,
当x=4时,ODCF的值最大,最大值为16,
设此时半径为r,则OA=OE=r,OD=8-r,
在Rt△ODE中,
∵OD2+DE2=OE2,
∴(8-r)2+42=r2,
解得r=5,
即此时半径长为5;
②△CEF的周长为定值,△CEF的周长=16,
在Rt△ODE中,OD2+DE2=OE2,OA=OE,
即:(8-OE)2+x2=OE2,
∴OE=4+![]() ,OD=8-OE=4-
,OD=8-OE=4-![]() ,
,
∵Rt△DOE∽Rt△CEF,
即![]() ,
,
∴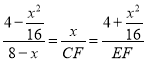 ,
,
解得:CF=![]() ,EF=
,EF=![]() ,
,
∴△CEF的周长=CE+CF+EF=8-x+![]() +
+![]() =16.
=16.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案