题目内容
如图，AB为⊙O的直径，过B作⊙O的切线，在该切线上取点C，连接AC交⊙O于D，若⊙O的半径是6，∠C=36°，则劣弧AD的长是（ ）A、
| ||
B、
| ||
C、
| ||
| D、3π |
练习册系列答案
名校课堂系列答案
相关题目
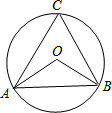如图，⊙O是等边△ABC的外接圆，则∠AOB等于（ ）| A、30° | B、60° | C、80° | D、120° |
如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，联结BC，若∠A=36°，则∠C等于（ ）| A、36° | B、54° | C、60° | D、27° |
如图，Rt△ABC内接于半圆O，∠C=90°，AC=6，BC=8．若在CB延长线上取一点D，过点D作半圆O的切线DE，当∠BDE=∠ABC时，BD的长为（ ）
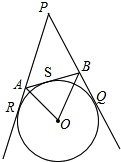如图，PQ、PR、AB是⊙O的切线，切点分别为Q、R、S，若∠APB=40°，则∠A0B等于（ ）| A、40° | B、50° | C、60° | D、70° |
Rt△ABC中，∠C=90°，以BC为直径的⊙O交AB于E，OD⊥BC交⊙O于D，DE交BC于F，点P为CB延长线上的一点，PE延长交AC于G，PE=PF．小华得出3个结论：①GE=GC；②AG=GE；③OG∥BE．
其中正确的是（ ）
| A、①② | B、①③ | C、②③ | D、①②③ |
若⊙O1的半径为6，⊙O2与⊙O1外切，圆心距O1O2=10，则⊙O2的半径为（ ）
| A、4 | B、16 | C、8 | D、4或16 |
在平面直角坐标系中，已知点A（0，2），⊙A的半径是2，⊙P的半径是1，满足与⊙A及x轴都相切的⊙P有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，下列说法不正确的是（ ）| A、△CDF的周长等于AD+CD | B、FC平分∠BFD | C、AC2+BF2=4CD2 | D、DE2=EF•CE |