题目内容
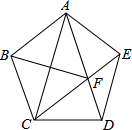如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，下列说法不正确的是（ ）| A、△CDF的周长等于AD+CD | B、FC平分∠BFD | C、AC2+BF2=4CD2 | D、DE2=EF•CE |
练习册系列答案
科学实验活动册系列答案
相关题目
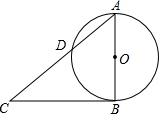如图，AB为⊙O的直径，过B作⊙O的切线，在该切线上取点C，连接AC交⊙O于D，若⊙O的半径是6，∠C=36°，则劣弧AD的长是（ ）A、
| ||
B、
| ||
C、
| ||
| D、3π |
已知⊙O1与⊙O2的半径R、r分别是方程x2-7x+12=0的两根，且圆心距d=1，那么⊙O1与⊙O2的位置关系是（ ）
| A、外离 | B、外切 | C、相交 | D、内切 |
已知⊙O1和⊙O2相切，两圆的圆心距为9cm，⊙O1的半径为4cm，则⊙O2的半径为（ ）
| A、5cm | B、13cm | C、9 cm 或13cm | D、5cm 或13cm |
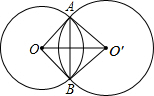如图，⊙O和⊙O′相交于A、B两点，且OO′=5，OA=3，O′B=4，则AB=（ ）| A、5 | B、2.4 | C、2.5 | D、4.8 |
⊙O的半径等于3，则⊙O的内接正方形的边长等于（ ）
| A、3 | ||
B、2
| ||
C、3
| ||
| D、6 |
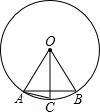如图，在⊙O中，OA=AB，OC⊥AB，交⊙O于点C，那么下列结论错误的是（ ）| A、∠BAC=30° | B、弧AC等于弧BC | C、线段OB的长等于圆内接正六边形的半径 | D、弦AC的长等于圆内接正十二边形的边长 |
已知一扇形的圆心角是60°，扇形的半径为9，则这个扇形的弧长是（ ）
| A、π | B、2π | C、3π | D、4π |
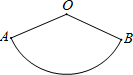如图，某同学用一扇形纸板为一个玩偶制作一个圆锥形帽子，已知扇形半径OA=13cm，扇形的弧长为10πcm，那么这个圆锥形帽子的高是（ ）cm．（不考虑接缝）