题目内容
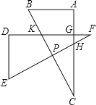
【题目】如图所示,△ABC为等边三角形,FB平分∠ABC,D为BF的中点,连接AD交BC的延长线于点E,若EF⊥BF,则![]() _______________
_______________

【答案】![]()
【解析】
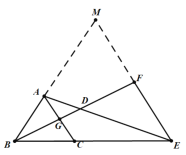
延长BA、EF交于点M,BD、AC交于点G,通过已知条件得到△AGD∽△EFD,利用对应边成比例求得CE的长,即可得到答案.
解:延长BA、EF交于点M,BD、AC交于点G,
∵△ABC为等边三角形,BF为角平分线,
∴∠EBF=30°,
又∵EF⊥BF,
∴∠BEF=60°,
∴△BME为等边三角形,
设BE=EM=BM=2,
∵BF⊥EM且BF为∠EBM角平分线,
∴EF=FM=1,BF=![]() ,
,
∵D为BF中点,
∴BD=DF=![]() ,
,
∵∠BCA=∠BEM=60°,
∴AC∥EM
∴△AGD∽△EFD
∴![]() ,
,
设AG为a,则DG=![]() a,AC=2a,
a,AC=2a,
易得BG=![]() a,
a,
则BG+GD=![]() a+
a+![]() a=
a=![]() ,
,
∴a=![]() ,
,
∴AC=BC=![]() ,
,
CE=BE-BC=2-![]() =
=![]() ,
,
∴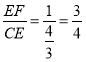 .
.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目