题目内容
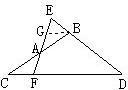 13、如图所示,△DEF中,DE=DF,过EF上一点A作直线与DE交于点B,与DF的延长线交于点C,且BE=CF.
13、如图所示,△DEF中,DE=DF,过EF上一点A作直线与DE交于点B,与DF的延长线交于点C,且BE=CF.求证:AB=AC.
证明:过B作BG∥CD交EF于G,∴∠EGB=∠EFD.∵DE=DF,∴
∠E=∠DFE
.∴
∠E=∠EGB,
.∴BE=BG.∵BE=CF,∴BG=CF.
∵BG∥CD,∴∠GBA=∠FCA,∠AGB=∠AFC.
∴△AGB≌△AFC.∴AB=AC.
阅读后回答下列问题:
(1)试在上述过程中的横线上填写适当的步骤;
(2)还有别的辅助线作法吗?若有,试说出一种:
过C作CH∥DE,交EF的延长线于H.
;(3)若DE=DF,AB=AC,则BE、CF之间有何关系?
(4)若AB=AC,BE=CF,DF=8cm,则DE的长为
8cm
;(5)若AB=m•AC,DE=DF,CF=a,则BE的长为
am
.分析:(1)由于DE=DF,利用等边对等角,可知∠E=∠EFD,再利用等量代换,可得∠E=∠EGB.
(2)过C作CH∥DE,交EF的延长线于H.
(3)BE=CF.过B作BG∥CD交EF于G,可先证△AGB≌△AFC,那么有BG=CF,再由BG∥CD,可得∠BGE=∠DFE,而BE=CF,故BE=BG,于是∠BGE=∠BEG,因此∠E=∠DFE,那么DE=DF.
(4)过B作BG∥CD交EF于G,先证△AGB≌△AFC,就有BG=CF,而BE=CF,所以BE=BG,可以知道∠E=∠BGE,再由BG∥CD,可得∠BGE=∠DFE,于是∠E=∠DFE,故DE=DF=8cm.
(5)过B作BG∥CD交EF于G,∠BGE=∠DFE,而DE=DF,可得∠E=∠DFE,那么就有∠E=∠BGE,于是BE=BG,再利用平行线分线段成比例定理的推论,可知△AGB∽△AFC,于是就有BG:CF=AB:AC,而BG=BE,那么BE:CF=AB:AC,就可求出BE.
(2)过C作CH∥DE,交EF的延长线于H.
(3)BE=CF.过B作BG∥CD交EF于G,可先证△AGB≌△AFC,那么有BG=CF,再由BG∥CD,可得∠BGE=∠DFE,而BE=CF,故BE=BG,于是∠BGE=∠BEG,因此∠E=∠DFE,那么DE=DF.
(4)过B作BG∥CD交EF于G,先证△AGB≌△AFC,就有BG=CF,而BE=CF,所以BE=BG,可以知道∠E=∠BGE,再由BG∥CD,可得∠BGE=∠DFE,于是∠E=∠DFE,故DE=DF=8cm.
(5)过B作BG∥CD交EF于G,∠BGE=∠DFE,而DE=DF,可得∠E=∠DFE,那么就有∠E=∠BGE,于是BE=BG,再利用平行线分线段成比例定理的推论,可知△AGB∽△AFC,于是就有BG:CF=AB:AC,而BG=BE,那么BE:CF=AB:AC,就可求出BE.
解答:解:(1)∠E=∠EFD,∠E=∠FGB;
(2)过点B作BH∥EF交CD于H;
(3)BE=CF;
(4)8cm;
(5)过B作BG∥CD交EF于G,
∵∠BGE=∠DFE,DE=DF,
∴∠E=∠DFE,
∴∠E=∠BGE,
∴BE=BG,
又∵BG∥CF,
∴△AGB∽△AFC,
∴BG:CF=AB:AC,
∴BE:CF=AB:AC,
∴BE=ma.
(2)过点B作BH∥EF交CD于H;
(3)BE=CF;
(4)8cm;
(5)过B作BG∥CD交EF于G,
∵∠BGE=∠DFE,DE=DF,
∴∠E=∠DFE,
∴∠E=∠BGE,
∴BE=BG,
又∵BG∥CF,
∴△AGB∽△AFC,
∴BG:CF=AB:AC,
∴BE:CF=AB:AC,
∴BE=ma.
点评:本题考查了三角形全等的判定及性质;本题主要是作辅助线,以及利用了全等三角形的判定和性质、相似三角形的判定和性质.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
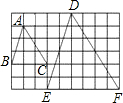 在如图所示方格纸中,已知△DEF是由△ABC经相似变换所得的像,那么△DEF的面积原面积比扩大了
在如图所示方格纸中,已知△DEF是由△ABC经相似变换所得的像,那么△DEF的面积原面积比扩大了 在如图所示方格纸中,已知△DEF是由△ABC经相似变换所得的像,那么△DEF的每条边都扩大到原来的
在如图所示方格纸中,已知△DEF是由△ABC经相似变换所得的像,那么△DEF的每条边都扩大到原来的 如图所示,△DEF中,DE=DF,过EF上一点A作直线与DE交于点B,与DF的延长线交于点C,且BE=CF.
如图所示,△DEF中,DE=DF,过EF上一点A作直线与DE交于点B,与DF的延长线交于点C,且BE=CF.