题目内容
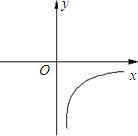 如图,曲线是反比例函数
如图,曲线是反比例函数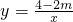 的图象的一支.
的图象的一支.
(1)图象另一支在第______象限;
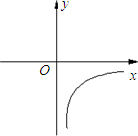
(2)m的取值范围是______;
(3)点A(-2,y1),B(-1,y2) 和C (1,y3) 都在这个反比例函数图象上,则y1,y2,y3的大小关系是______
A、y1<y2<y3 ;B、y3<y1<y2;C、y1>y2,>y3;D、y1<y3<y2.
解:(1)由反比例函数的图象可知,函数图象一支位于第四象限,故可知另一支位于第二象限,
(2)∵反比例函数的图象位于二、四象限,
∴4-2m<0,
解得m>2,
(3):∵反比例函数的系数k<0,
∴此函数的图象在二、四象限,
∵-2<0,-1<0,1>0,
∴(-2,y1),(-1,y2)在第二象限,(1,y3)在第四象限,
∴y1>0,y2>0,y3<0,
∵-4<-2,
∴y2>y1>0,
∴y3<y1<y2.
故答案为二、m>2、B.
分析:(1)根据图象可知,函数图象一支位于第四象限,故可知另一支位于第二象限,
(2)当反比例函数系数k<0时,图象位于二、四象限,故可列不等式4-2m<0,解得m的取值范围即可,
(3)由反比例函数的图象在二、四象限,由三点的横坐标可知(-2,y1),(-1,y2)在第二象限,(1,y3)在第四象限,根据反比例函数的增减性及各象限内点的坐标特点即可解答.
点评:本题主要考查反比例函数的图象和反比例函数的性质等知识点,解答此题的关键是熟练掌握反比例函数的性质,当系数k<0时,反比例函数图象位于二、四象限,当k>0时,函数图象位于一、三象限.
(2)∵反比例函数的图象位于二、四象限,
∴4-2m<0,
解得m>2,
(3):∵反比例函数的系数k<0,
∴此函数的图象在二、四象限,
∵-2<0,-1<0,1>0,
∴(-2,y1),(-1,y2)在第二象限,(1,y3)在第四象限,
∴y1>0,y2>0,y3<0,
∵-4<-2,
∴y2>y1>0,
∴y3<y1<y2.
故答案为二、m>2、B.
分析:(1)根据图象可知,函数图象一支位于第四象限,故可知另一支位于第二象限,
(2)当反比例函数系数k<0时,图象位于二、四象限,故可列不等式4-2m<0,解得m的取值范围即可,
(3)由反比例函数的图象在二、四象限,由三点的横坐标可知(-2,y1),(-1,y2)在第二象限,(1,y3)在第四象限,根据反比例函数的增减性及各象限内点的坐标特点即可解答.
点评:本题主要考查反比例函数的图象和反比例函数的性质等知识点,解答此题的关键是熟练掌握反比例函数的性质,当系数k<0时,反比例函数图象位于二、四象限,当k>0时,函数图象位于一、三象限.

练习册系列答案
相关题目
 如图,曲线是反比例函数
如图,曲线是反比例函数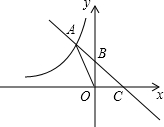 (2012•中江县二模)如图中曲线是反比例函数
(2012•中江县二模)如图中曲线是反比例函数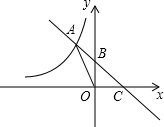 如图中曲线是反比例函数
如图中曲线是反比例函数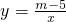 的图象的一条.
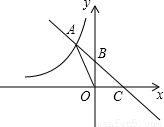
的图象的一条.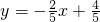 的图象与反比例函数的图象交于点A,与y轴、x轴分别交于点B、C,如图所示.已知△AOC的面积为2,求m的值;
的图象与反比例函数的图象交于点A,与y轴、x轴分别交于点B、C,如图所示.已知△AOC的面积为2,求m的值;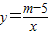 的图象的一条.
的图象的一条.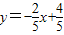 的图象与反比例函数的图象交于点A,与y轴、x轴分别交于点B、C,如图所示.已知△AOC的面积为2,求m的值;
的图象与反比例函数的图象交于点A,与y轴、x轴分别交于点B、C,如图所示.已知△AOC的面积为2,求m的值;