题目内容
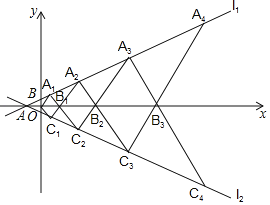
【题目】如图,在平面直角坐标系中,直线l2:![]() 与x轴交于点A;与y轴交于点B,以x轴为对称轴作直线
与x轴交于点A;与y轴交于点B,以x轴为对称轴作直线![]() 的轴对称图形的直线l2,点A1,A2,A3…在直线l1上,点B1,B2,B3…在x正半轴上,点C1,C2,C3…在直线l2上,若△A1B1O、△A2B2B1、△A2B1B2、…△AnBnBn﹣1均为等边三角形,四边形A1B1C1O、四边形A2B2C2B1、四边形A2B1C2B2…、四边形AnBnnBn﹣1的面积分别是S1、S2、S3、…、Sn,则Sn为_____.(用含有n的代数式表示)
的轴对称图形的直线l2,点A1,A2,A3…在直线l1上,点B1,B2,B3…在x正半轴上,点C1,C2,C3…在直线l2上,若△A1B1O、△A2B2B1、△A2B1B2、…△AnBnBn﹣1均为等边三角形,四边形A1B1C1O、四边形A2B2C2B1、四边形A2B1C2B2…、四边形AnBnnBn﹣1的面积分别是S1、S2、S3、…、Sn,则Sn为_____.(用含有n的代数式表示)
【答案】![]()
【解析】
依据直线l1:y=![]() x+1,可得∠BAO=30°,进而得出∠AA1O=30°,AO=A1O=
x+1,可得∠BAO=30°,进而得出∠AA1O=30°,AO=A1O=![]() ,得到
,得到![]() =
=![]() ×
×![]() ×
×![]() ×
×![]() =
=![]() ,由轴对称图形可得,S1=2S△A1OB1=
,由轴对称图形可得,S1=2S△A1OB1=![]() ,分别求得四边形A1B1C1O、四边形A2B2C2B1、四边形A3B3C3B2的对角线的长,求得面积,根据规律可得四边形AnBnCnBn-1的面积,
,分别求得四边形A1B1C1O、四边形A2B2C2B1、四边形A3B3C3B2的对角线的长,求得面积,根据规律可得四边形AnBnCnBn-1的面积,
由直线l1:![]() ,可得A(﹣
,可得A(﹣![]() ,0),B(0,1),
,0),B(0,1),
∴AO=![]() ,BO=1,
,BO=1,
∴∠BAO=30°,
又∵∠A1OB1=60°,
∴∠AA1O=30°,
∴AO=A1O=![]() ,
,
∴OB1=A1O=![]() ,
,
∴![]() ,
,
由轴对称图形可得,S1=![]() ,
,
同理可得,AB1=A2B1=2![]() ,S2=
,S2=![]() ,
,
以此类推,Sn=22n﹣33![]() ,
,

练习册系列答案
相关题目