题目内容
阅读下列文字与例题
将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法。
例如：⑴am+an+bm+bn=(am+bm)+(an+bn)
=m(a+b)+n(a+b)
=(a+b)(m+n)
⑵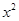
-
-
-
=
=
=
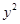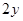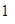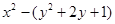
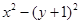
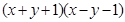
试用上述方法分解因式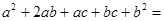
。
将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法。
例如：⑴am+an+bm+bn=(am+bm)+(an+bn)
=m(a+b)+n(a+b)
=(a+b)(m+n)
⑵
---==
=
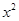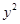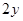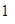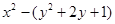
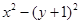
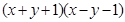
试用上述方法分解因式
。
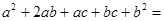首先进行合理分组，然后运用提公因式法和公式法进行因式分解．
解：原式=（a2+2ab+b2）+（ac+bc）
=（a+b）2+c（a+b）
=（a+b）（a+b+c）．
故答案为（a+b）（a+b+c）．
此题考查了因式分解法，要能够熟练运用分组分解法、提公因式法和完全平方公式．
解：原式=（a2+2ab+b2）+（ac+bc）
=（a+b）2+c（a+b）
=（a+b）（a+b+c）．
故答案为（a+b）（a+b+c）．
此题考查了因式分解法，要能够熟练运用分组分解法、提公因式法和完全平方公式．
练习册系列答案
相关题目
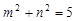，那么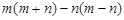
的值是 ▲ ．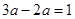
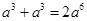
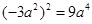
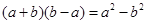
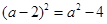
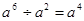
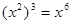
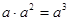
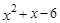的是（ ）．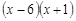
、
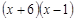
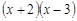
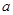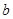，定义运算☆如下：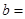
，
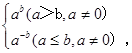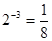.计算[2☆(
)]
[(
)]=___________.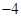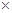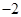