题目内容
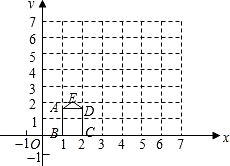 如图,矩形ABCD的长,宽分别为
如图,矩形ABCD的长,宽分别为| 3 |
| 2 |
| 3 |
| 2 |
(1)求经过A,E,D三点的抛物线的表达式;
(2)若以原点为位似中心,将五边形AEDCB放大,使放大后的五边形的边长是原五边形对应边长的3倍,请在下图网格中画出放大后的五边形A′E′D′C′B′;
(3)经过A′,E′,D′三点的抛物线能否由(1)中的抛物线平移得到?请说明理由.
分析:(1)A,E,D三点坐标已知,可用一般式来求解;
(2)延长OA到A′,使OA′=3OA,同理可得到其余各点;
(3)根据二次项系数是否相同即可判断两个函数是否由平移得到.
(2)延长OA到A′,使OA′=3OA,同理可得到其余各点;
(3)根据二次项系数是否相同即可判断两个函数是否由平移得到.
解答: 解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c
解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c
∵A(1,
),E(
,2),D(2,
)(1分)
∴
,解之,得
∴过A,E,D三点的抛物线的表达式为y=-2x2+6x-
.(4分)
(2)如图.(7分)
(3)不能,理由如下:(8分)
设经过A′,E′,D′三点的抛物线的表达式为y=a′x2+b′x+c′
∵A′(3,
),E′(
,6),D′(6,
)
∴
,
解之,得a′=-
a=-2,a′=-
,
∴a≠a′
∴经过A′,E′,D′三点的抛物线不能由(1)中的抛物线平移得到.(8分)
 解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c
解:(1)设经过A,E,D三点的抛物线的表达式为y=ax2+bx+c∵A(1,
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴
|
|
∴过A,E,D三点的抛物线的表达式为y=-2x2+6x-
| 5 |
| 2 |
(2)如图.(7分)
(3)不能,理由如下:(8分)
设经过A′,E′,D′三点的抛物线的表达式为y=a′x2+b′x+c′
∵A′(3,
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
∴
|
解之,得a′=-
| 2 |
| 3 |
a=-2,a′=-
| 2 |
| 3 |
∴a≠a′
∴经过A′,E′,D′三点的抛物线不能由(1)中的抛物线平移得到.(8分)
点评:一般用待定系数法来求函数解析式;位似变化的方法应熟练掌握;抛物线平移不改变a的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
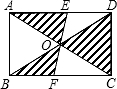 如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为
如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为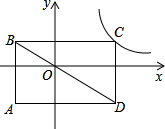 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=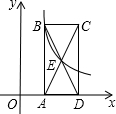 如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线
如图,矩形ABCD的一边AD在x轴上,对角线AC、BD交于点E,过B点的双曲线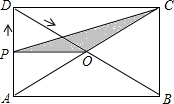 (2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( )
(2013•葫芦岛)如图,矩形ABCD的对角线交于点O,∠BOC=60°,AD=3,动点P从点A出发,沿折线AD-DO以每秒1个单位长的速度运动到点O停止.设运动时间为x秒,y=S△POC,则y与x的函数关系大致为( )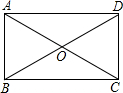 如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=
如图,矩形ABCD的对角线交于O点,∠AOB=120°,AD=5cm,则AC=