题目内容
阅读并填空:
(1)方程x2+2x+1=0的根为x1=______,x2=______,x1+x2=______,x1x2=______;
(2)方程x2-2x-3=0的根为x1=______,x2=______,x1+x2=______,x1x2=______;
(3)方程3x2+2x-5=0的根为x1=______,x2=______,x1+x2=______,x1x2=______;
(4)由(1)(2)(3)你能得出什么猜想?
(5)利用你的猜想解决问题:已知方程2x2+3x-5=0的两根为x1、x2,求 的值.
的值.
解:
(1)∵x2+2x+1=0,∴(x+1)2=0,解得x1=x2=-1,∴x1+x2=-2,x1x2=1;
(2)∵x2-2x-3=0,∴(x-3)(x+1)=0,解得x1=3,x2=-1,∴x1+x2=2,x1x2=-3;
(3)∵3x2+2x-5=0,∴(x-1)(3x+5)=0,解得x1=1,x2=- ,∴x1+x2=-
,∴x1+x2=- ,x1x2=-
,x1x2=- ;
;
(4)设ax2+bx+c=0(a≠0,且a、b、c是常数)的两根为x1、x2,则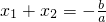 ,
,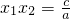 ;
;
(5)解:∵ ,
,
∴ .
.
分析:(1)、(2)、(3)利用因式分解法求解方程的两根,再根据方程的两根可求出x1+x2,x1x2的值;
(4)可以先设方程的两根是x1、x2,那么就有x1+x2=- ,x1•x2=
,x1•x2= ;
;
(5)先利用根与系数的关系求出x1+x2,x1•x2的值,根据 =
= ,然后整体代入通分后的式子求值即可.
,然后整体代入通分后的式子求值即可.
点评:一元二次方程的两个根x1、x2具有这样的关系:x1+x2=- ,x1•x2=
,x1•x2= .
.
(1)∵x2+2x+1=0,∴(x+1)2=0,解得x1=x2=-1,∴x1+x2=-2,x1x2=1;
(2)∵x2-2x-3=0,∴(x-3)(x+1)=0,解得x1=3,x2=-1,∴x1+x2=2,x1x2=-3;
(3)∵3x2+2x-5=0,∴(x-1)(3x+5)=0,解得x1=1,x2=-
 ,∴x1+x2=-
,∴x1+x2=- ,x1x2=-
,x1x2=- ;
;(4)设ax2+bx+c=0(a≠0,且a、b、c是常数)的两根为x1、x2,则
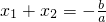 ,
,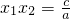 ;
;(5)解:∵
 ,
,
∴
 .
.分析:(1)、(2)、(3)利用因式分解法求解方程的两根,再根据方程的两根可求出x1+x2,x1x2的值;
(4)可以先设方程的两根是x1、x2,那么就有x1+x2=-
 ,x1•x2=
,x1•x2= ;
;(5)先利用根与系数的关系求出x1+x2,x1•x2的值,根据
 =
= ,然后整体代入通分后的式子求值即可.
,然后整体代入通分后的式子求值即可.点评:一元二次方程的两个根x1、x2具有这样的关系:x1+x2=-
 ,x1•x2=
,x1•x2= .
. 
练习册系列答案
相关题目
 nB,AD=bsinC,于是csinB=bsinC,即
nB,AD=bsinC,于是csinB=bsinC,即 到0.1.参考数据:sin40°=0.643,sin65°=0.90 6,sin70°=0.940,sin75°=0.966).
到0.1.参考数据:sin40°=0.643,sin65°=0.90 6,sin70°=0.940,sin75°=0.966). ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 .
. ,
, .
. …(*)
…(*) ______
______ ∠B;
∠B; ______
______ ∠C;
∠C; ______
______ c.
c.

 ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 .
. ,
, .
. …(*)
…(*) ______
______ ∠B;
∠B; ______
______ ∠C;
∠C; ______
______ c.
c.

 ,sinC=
,sinC= ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 .
. ,
, .
. …(*)
…(*)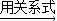 ______
______ ∠B;
∠B; ______
______ ∠C;
∠C; ______
______ c.
c.

 ,sinC=
,sinC=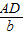 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 .
. ,
, .
. …(*)
…(*) ______
______ ∠B;
∠B; ______
______ ∠C;
∠C; ______
______ c.
c.
