题目内容
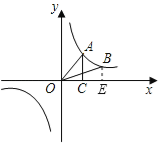
【题目】如图,点A、B在反比例函数![]() 的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
的图象上,且点A、B的横坐标分别为a、2a(a>0),AC⊥x轴,垂足为C,且△AOC的面积为2,
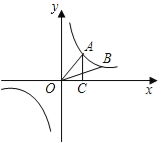
(1)求该反比例函数的解析式;
(2)求△AOB的面积.
【答案】(1)y=![]() ;(2)3.
;(2)3.
【解析】试题分析:(1)由S△AOC=![]() xy=2,设反比例函数的解析式y=
xy=2,设反比例函数的解析式y=![]() ,则k=xy=4;
,则k=xy=4;
(2)连接AB,过点B作BE⊥x轴,交x轴于E点,通过分割面积法S△AOB=S△AOC+S梯形﹣S△BOE求得.
解:(1)∵S△AOC=2,
∴k=2S△AOC=4;
∴y=![]() ;
;
(2)连接AB,过点B作BE⊥x轴,
S△AOC=S△BOE=2,
∴A(a,![]() ),B(2a,
),B(2a,![]() );
);
S梯形ACEB=![]() (
(![]() +
+![]() )×(2a﹣a)=3,
)×(2a﹣a)=3,
∴S△AOB=S△AOC+S梯形ACEB﹣S△BOE=3.

练习册系列答案
相关题目