题目内容
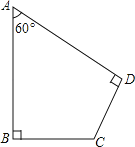
【题目】如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积.
【答案】![]() .
.
【解析】
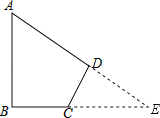
试题分析:延长AD、BC交于E,根据直角三角形两锐角互余求出∠E=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出AE、CE,再利用勾股定理列式求出BE、DE,然后根据四边形的面积等于两个直角三角形的面积的差列式计算即可得解.
如图,延长AD、BC交于E.
∵∠B=90°,∠A=60°,
∴∠E=90°﹣60°=30°,
在Rt△ABE和Rt△CDE中,∵AB=2,CD=1,
∴AE=2AB=2×4,CE=2CD=2×1=2,
由勾股定理得,BE=![]() =2
=2![]() ,
,
DE=![]() =
=![]() ,
,
∴S四边形ABCD=![]() ×2
×2![]() ×2﹣
×2﹣![]() ×
×![]() ×1,
×1,
=2![]() ﹣
﹣![]() ,
,
=![]() .
.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
【题目】某商店 3 月份、4 月份出售同一品牌各种规格的空调台数如下表;根据表中的数据 回答下列问题:
规格 月份 | A 型号 | B 型号 | C 型号 | D 型号 |
三月 | 12台 | 20台 | 8台 | 4台 |
四月 | 16台 | 30台 | 8台 | 6台 |
(1)商店这两个月平均每月销售空调____台;
(2)请你帮助该商店经理考虑下,6月份进货时,商店对____型号的空调要多进,对_______型号的空调要少进.