题目内容
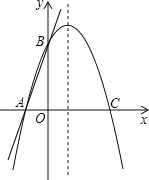
【题目】如图,直线![]() 交
交![]() 轴于A点,交
轴于A点,交![]() 轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
⑴求抛物线的解析式;
⑵在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
【答案】(1)此抛物线的解析式为y=-(x+1)(x-3)=-x2+2x+3;
(2)Q点坐标为(1,1),(1,0),(1,![]() ),(1,﹣
),(1,﹣![]() ).
).
【解析】
(1)根据直线的解析式y=3x+3,当x=0和y=0时就可以求出点A、B的坐标,设抛物线的解析式为y=ax2+bx+c,根据A、B、C三点的坐标利用待定系数法就可以求出抛物线的解析式;
(2)将抛物线化为顶点式,求出对称轴对称轴,设出Q点的坐标,利用等腰三角形的性质,根据两点间的距离公式就可以求出Q点的坐标.
(1)∵y=3x+3,
∴当x=0时,y=3,当y=0时,x=﹣1,
∴A(﹣1,0),B(0,3).
设抛物线的解析式为y=ax2+bx+c,由题意,得
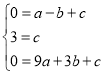 ,
,
解得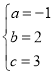
∴抛物线的解析式为:y=﹣x2+2x+3
(2)∵y=﹣x2+2x+3,
∴y=﹣(x﹣1)2+4
∴抛物线的对称轴为x=1,设Q(1,a),
①当AQ=BQ时,如图,
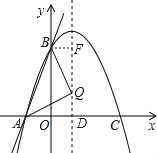
由勾股定理可得
BQ=![]() ,
,
AQ=![]()
得![]() ,
,
解得a=1,
∴Q(1,1);
②如图:
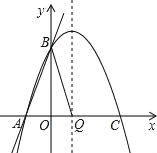
当AB是腰时,Q是对称轴与x轴交点时,AB=BQ,
∴![]()
![]()
解得:a=0或6,
当Q点的坐标为(1,6)时,其在直线AB上,A、B和Q三点共线,舍去,
则此时Q的坐标是(1,0);
③当AQ=AB时,如图:
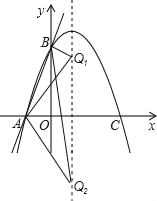
![]() ,解得a=±
,解得a=±![]() ,则Q的坐标是(1,
,则Q的坐标是(1,![]() )和(1,﹣
)和(1,﹣![]() ).
).
综上所述:Q点坐标为(1,1),(1,0),(1,![]() ),(1,﹣
),(1,﹣![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】己知二次函数y=ax2+bx+c的y与x的部分对应值如下表;
x | -1 | 0 | 1 | 3 |
y | -3 | 1 | 3 | 1 |
下列结论:①抛物线的开口向下;②其图象的对称轴为x=1;③当x﹤l时,函数值y随x 的增大而增大;④方程ax2+bx+c=0有一个根大于4.其中正确的结论有( )
A. 4个B. 1个C. 3个D. 2个