题目内容
【题目】在△ABC中，AB=AC，AB的垂直平分线DE与AC所在的直线相交于点E，垂足为D，连接BE．已知AE=5，tan∠AED=
，求BE+CE的值
【答案】BE+CE=6或16
【解析】
本题有两种情形，需要分类讨论．首先根据题意画出图形，由线段垂直平分线的性质，即可求得AE=BE，又由三角函数的性质，求得AD的长，继而求得答案．
解：有两种情形，需要分类讨论：
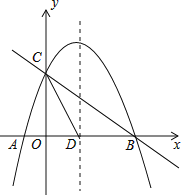
①∠BAC为锐角，如图所示，
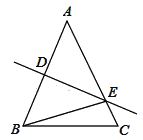
∵AB的垂直平分线是DE，
∴AE=BE，ED⊥AB，
∵AE=5，tan∠AED
∴sin∠AED
∴AD=AEsin∠AED=3．
∴AB=6．
∴BE+CE=AE+CE=AC=AB=6．
②若∠BAC为钝角，如图所示，同理可求得：BE+CE=16．
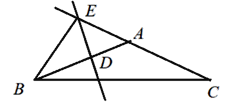
综上所述，BE+CE=6或16
练习册系列答案
同步练习强化拓展系列答案
相关题目
