题目内容
 如图,有一个圆柱,它的高为12厘米,底面半径为3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则需要爬行的最短路程是
如图,有一个圆柱,它的高为12厘米,底面半径为3厘米,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则需要爬行的最短路程是15
15
厘米.(π的值取3)分析:要想求得最短路程,首先要把A和B展开到一个平面内.根据两点之间,线段最短求出蚂蚁爬行的最短路程.
解答: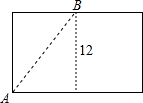 解:展开圆柱的半个侧面是矩形,
解:展开圆柱的半个侧面是矩形,
矩形的长是圆柱的底面周长的一半,即3π≈9,矩形的宽是圆柱的高12.
根据两点之间线段最短,
知最短路程是矩形的对角线的长,即
=15厘米.
故答案为:15.
 解:展开圆柱的半个侧面是矩形,
解:展开圆柱的半个侧面是矩形,矩形的长是圆柱的底面周长的一半,即3π≈9,矩形的宽是圆柱的高12.
根据两点之间线段最短,
知最短路程是矩形的对角线的长,即
| 122+92 |
故答案为:15.
点评:此题主要考查了平面展开图中最短路径求法,两个不在同一平面内的两个点之间的最短距离时,一定要展开到一个平面内.根据两点之间,线段最短.确定要求的长,再运用勾股定理进行计算.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
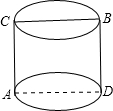 如图,有一个圆柱,它的高为9cm,底面半径为4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则沿着圆柱的表面需要爬行的最短路程是
如图,有一个圆柱,它的高为9cm,底面半径为4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面B点处的食物,则沿着圆柱的表面需要爬行的最短路程是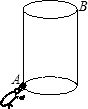 如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是
如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是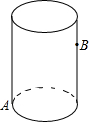 如图,有一个圆柱,它的高为13cm,底面周长为10cm,在圆柱的下底面上A点处有一个蚂蚁想吃到离上底面1cm处的B点的食物,需爬行的最短距离为
如图,有一个圆柱,它的高为13cm,底面周长为10cm,在圆柱的下底面上A点处有一个蚂蚁想吃到离上底面1cm处的B点的食物,需爬行的最短距离为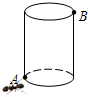 如图,有一个圆柱,它的高等于8cm,底面半径等于2
如图,有一个圆柱,它的高等于8cm,底面半径等于2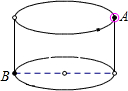 如图,有一个圆柱,它的高为15cm,底面半径为
如图,有一个圆柱,它的高为15cm,底面半径为