题目内容
已知:如图,抛物线y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
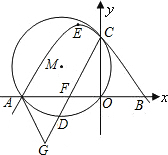 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧 |
| OA |
(1)求抛物线的顶点E的坐标;
(2)求⊙M的面积;
(3)连CD交AO于点F,延长CD至G,使FG=2,试探究,当点D运动到何处时,直线GA与⊙M相切,并请说明理由.
分析:(1)已知了抛物线的解析式,用配方法和公式法求都可以.
(2)由于∠AOC是直角,那么连接AC,则AC必过圆心M,也就是说AC就是圆M的直径,因此求出AC就可以得出圆M的半径长,根据抛物线的解析式可求出A,C两点的坐标,也就知道了OA,OC的长,可在直角三角形AOC中,用勾股定理求出AC,然后可根据圆的面积的计算公式求出圆M的面积.
(3)应是D到OA中点时,GA与圆M相切,要证垂直就必须证AC⊥AG,此时D是弧OA的中点,根据OC,OA的长,不难得出∠ACO=60°,那么∠FCO=∠ACD=30°,有OC=
,那么可求得OF=1,AF=OA-OF=2,首先三角形AFG是个等腰三角形,而∠CFO=90-30=60°,因此∠AFG=60°,三角形AFG就是个等边三角形,∠FAG=60°,因此∠CAG=60+30=90°,即可得出GA与圆M相切.
(2)由于∠AOC是直角,那么连接AC,则AC必过圆心M,也就是说AC就是圆M的直径,因此求出AC就可以得出圆M的半径长,根据抛物线的解析式可求出A,C两点的坐标,也就知道了OA,OC的长,可在直角三角形AOC中,用勾股定理求出AC,然后可根据圆的面积的计算公式求出圆M的面积.
(3)应是D到OA中点时,GA与圆M相切,要证垂直就必须证AC⊥AG,此时D是弧OA的中点,根据OC,OA的长,不难得出∠ACO=60°,那么∠FCO=∠ACD=30°,有OC=
| 3 |
解答: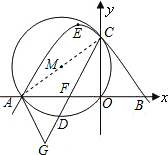 解:(1)抛物线y=-
解:(1)抛物线y=-
x2-
x+
=-
(x2+2x+1)+
+
=-
(x+1)2+
∴E的坐标为(-1,
);
(2)连AC;
∵⊙M过A,O,C,∠AOC=90°,
∴AC为⊙O的直径.
而|OA|=3,OC=
∴r=
=
.
∴S⊙M=πr2=3π;
(3)当点D运动到
的中点时,直线GA与⊙M相切.
理由:在Rt△ACO中,|OA|=3,OC=
,
∵tan∠ACO=
=
.
∴∠ACO=60°,∠CAO=30°.
∵点D是
的中点,
∴
=
.
∴∠ACG=∠DCO=30°.
∴OF=OC•tan30°=1,∠CFO=60°.
在△GAF中,AF=2,FG=2,∠AFG=∠CFO=60°,
∴△AGF为等边三角形.
∴∠GAF=60°.
∴∠CAG=∠GAF+∠CAO=90°.
又AC为直径,
∴当D为
的中点时,GA为⊙M的切线.
 解:(1)抛物线y=-
解:(1)抛物线y=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
=-
| ||
| 3 |
| 3 |
| ||
| 3 |
=-
| ||
| 3 |
4
| ||
| 3 |
∴E的坐标为(-1,
4
| ||
| 3 |
(2)连AC;
∵⊙M过A,O,C,∠AOC=90°,
∴AC为⊙O的直径.
而|OA|=3,OC=
| 3 |
∴r=
| AC |
| 2 |
| 3 |
∴S⊙M=πr2=3π;
(3)当点D运动到
 |
| OA |
理由:在Rt△ACO中,|OA|=3,OC=
| 3 |
∵tan∠ACO=
| 3 | ||
|
| 3 |
∴∠ACO=60°,∠CAO=30°.
∵点D是
 |
| OA |
∴
 |
| AD |
 |
| DO |
∴∠ACG=∠DCO=30°.
∴OF=OC•tan30°=1,∠CFO=60°.
在△GAF中,AF=2,FG=2,∠AFG=∠CFO=60°,
∴△AGF为等边三角形.
∴∠GAF=60°.
∴∠CAG=∠GAF+∠CAO=90°.
又AC为直径,
∴当D为
 |
| OA |
点评:本题将抛物线与圆放在同一坐标系中研究,因此数形结合的解题思想是不可缺少的,解第3小问时可以先自己作图来确定D点的位置.

练习册系列答案
相关题目
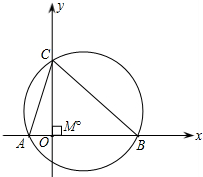 与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.
与y轴交点C的纵坐标为3,△ABC的外接圆的圆心为点M.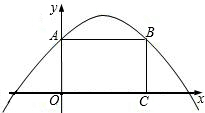 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12,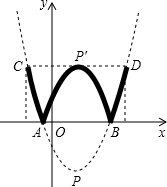 (2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(
(2013•宁化县质检)已知:如图,抛物线y=ax2+bx+c与x轴交于点A(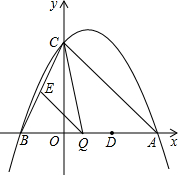 已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).
已知,如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A,B,点A的坐标为(4,0).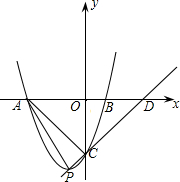 已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.
已知,如图,抛物线y=x2+px+q与x轴相交于A、B两点,与y轴交于点C,且OA≠OB,OA=OC,设抛物线的顶点为点P,直线PC与x轴的交点D恰好与点A关于y轴对称.