题目内容
 如图,点A在双曲线y=
如图,点A在双曲线y=| 4 |
| x |
| 1 |
| x |
| 9 |
| 8 |
| 9 |
| 8 |
分析:根据双曲线y=
设点A的坐标为(a,
),根据AB∥x轴,AC∥y轴判断出△ABC是直角三角形,并求出点B、C的坐标,从而求出AB、AC的长度,再利用三角形的面积公式列式计算即可得解.
| 4 |
| x |
| 4 |
| a |
解答:解:∵点A在双曲线y=
上,
∴设点A坐标为(a,
),
∵AB∥x轴,AC∥y轴,
∴△ABC是直角三角形,
∵AB∥x轴,
∴
=
,
解得x=
,
∴点B的坐标为(
,
),
∴AB=a-
=
,
∵AC∥y轴,
∴y=
,
∴点C的坐标为(a,
),
∴AC=
-
=
,
∴S△ABC=
AB•AC=
×
×
=
.
故答案为:
.
| 4 |
| x |
∴设点A坐标为(a,
| 4 |
| a |
∵AB∥x轴,AC∥y轴,
∴△ABC是直角三角形,
∵AB∥x轴,
∴
| 1 |
| x |
| 4 |
| a |
解得x=
| a |
| 4 |
∴点B的坐标为(
| a |
| 4 |
| 4 |
| a |
∴AB=a-
| a |
| 4 |
| 3a |
| 4 |
∵AC∥y轴,
∴y=
| 1 |
| a |
∴点C的坐标为(a,
| 1 |
| a |
∴AC=
| 4 |
| a |
| 1 |
| a |
| 3 |
| a |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3a |
| 4 |
| 3 |
| a |
| 9 |
| 8 |
故答案为:
| 9 |
| 8 |
点评:本题考查了反比例函数系数k的几何意义,利用点A的坐标分别求出点B、C的坐标是解题的关键.

练习册系列答案
相关题目
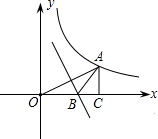 如图,点A在双曲线y=
如图,点A在双曲线y=| 6 |
| x |
A、2
| ||
| B、5 | ||
C、4
| ||
D、
|
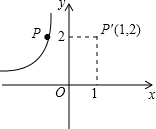 (2012•镇赉县模拟)如图,点P在双曲线
(2012•镇赉县模拟)如图,点P在双曲线 (2012•三明)如图,点A在双曲线
(2012•三明)如图,点A在双曲线 如图,点A在双曲线
如图,点A在双曲线