题目内容
在达成铁路复线工程中,某路段需要铺轨.先由甲工程队独做2天后,再由乙工程队独做3天刚好完成这项任务.已知乙工程队单独完成这项任务比甲工程队单独完成这项任务多用2天,求甲、乙工程队单独完成这项任务各需要多少天?
【答案】分析:求的是工作时间,工效已知,一定是根据工作总量为1,来列等量关系,本题的关键描述语是:甲工程队独做2天后,再由乙工程队独做3天刚好完成这项任务.等量关系为:甲做2天的工作量+乙做3天的工作量=1.
解答:解:设甲工程队单独完成任务需x天,则乙工程队单独完成任务需(x+2)天,(1分)
依题意得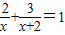 (4分)
(4分)
化为整式方程得x2-3x-4=0(5分)
(x+1)(x-4)=0
解得x=-1或x=4(6分)
检验:当x=4和x=-1时,x(x+2)≠0,∴x=4和x=-1都是原分式方程的解.
但x=-1不符合实际意义,故x=-1舍去;(7分)
∴乙单独完成任务需要x+2=6(天).
答:甲、乙工程队单独完成任务分别需要4天、6天.(8分)
点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.此题涉及的公式:工作总量=工作效率×工作时间.
解答:解:设甲工程队单独完成任务需x天,则乙工程队单独完成任务需(x+2)天,(1分)
依题意得
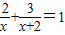 (4分)
(4分)化为整式方程得x2-3x-4=0(5分)
(x+1)(x-4)=0
解得x=-1或x=4(6分)
检验:当x=4和x=-1时,x(x+2)≠0,∴x=4和x=-1都是原分式方程的解.
但x=-1不符合实际意义,故x=-1舍去;(7分)
∴乙单独完成任务需要x+2=6(天).
答:甲、乙工程队单独完成任务分别需要4天、6天.(8分)
点评:本题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.此题涉及的公式:工作总量=工作效率×工作时间.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目