题目内容
为了美化校园,学校准备利用一面墙(墙足够长)和20米的篱笆围成一个如图所示的等腰梯形的花圃,设腰长AB=CD=X米,∠B=120。,花圃的面积为S平方米。
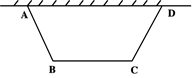
小题1:)求S与X的函数关系式
小题2:若梯形ABCD的面积为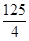
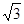 平方米,且AB﹤BC,求此时AB的长。
平方米,且AB﹤BC,求此时AB的长。

小题1:)求S与X的函数关系式
小题2:若梯形ABCD的面积为
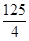
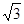 平方米,且AB﹤BC,求此时AB的长。
平方米,且AB﹤BC,求此时AB的长。小题1:S=
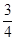
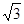
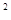 +10
+10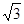 X
X小题2:-
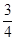
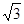
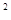 +10
+10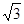 X =
X =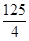
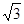 X1=5, X2=
X1=5, X2=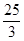 BC=20-
BC=20-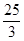 ×2=
×2= ∠AB ∴X =5
∠AB ∴X =5解:(1)由题意解得
等腰梯形的高为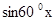
∴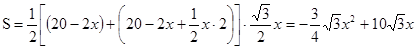
(2)代入面积值解:
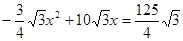
解得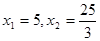
BC=20-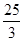 ×2=
×2=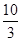 <AB
<AB
∴x=5,BC=20-10=10,
即AB的长为5.
本题考查了根据实际问题列二次函数关系式,本题先求得等腰梯形的高,求得关系式从而很容易解.
等腰梯形的高为
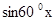
∴
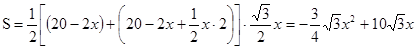
(2)代入面积值解:
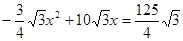
解得
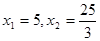
BC=20-
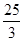 ×2=
×2=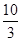 <AB
<AB∴x=5,BC=20-10=10,
即AB的长为5.
本题考查了根据实际问题列二次函数关系式,本题先求得等腰梯形的高,求得关系式从而很容易解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 米,则可列方程为 .
米,则可列方程为 .
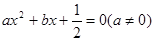 有两个相等的实数根,求
有两个相等的实数根,求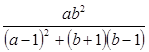 的值.
的值. 的解是
的解是 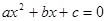 的两个根是-3和1,那么二次函数
的两个根是-3和1,那么二次函数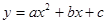 的图象的对称轴是直线( ).
的图象的对称轴是直线( ).  =-3
=-3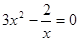
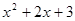
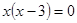
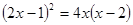
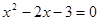 (考查一元二次方程的解法)
(考查一元二次方程的解法)