题目内容
同一直线上有A、B、C、D四点，AD=
DB，AC=
CB，且CD=4cm，则AB的长
或14
或14．
| 5 |
| 9 |
| 9 |
| 5 |
| 112 |
| 53 |
| 112 |
| 53 |
分析：分为两种情况（1）当B在D的右边时，求出AB=AD+DB=
AD，AC=
CB，①当B在C的右边时，求出AD=BC，得出
CB=CB+4，求出BC即可；②当B在C的左边时，有AB=AC-BC=
BC，得出DC=
AD+
AD，求出AD即可；（2）同理当B在D的左边时，求出BC=AD，代入得出方程，求出即可．
| 14 |
| 5 |
| 9 |
| 5 |
| 9 |
| 5 |
| 4 |
| 5 |
| 9 |
| 5 |
| 7 |
| 2 |
解答：解：∵AD=
DB
∴BD=
AD
（1）当B在D的右边时，
有AB=AD+DB=
AD，
∵AC=
CB，
①当B在C的右边时，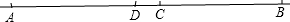
∵此时AB=AC+CB=
BC
∴AD=BC，
∵AC=AD+DC=BC+DC，
CB=CB+4，
即BC=5，
∴AB=14
②当B在C的左边时，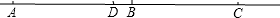
有AB=AC-BC=
BC-BC=
BC，
∵AD=
DB，
∴
=
，
∵DC=DB+BC=DB+
AD=
AD+
AD
解得AD=
AB=
；
（2）同理当B在D的左边时，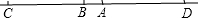
∵AD=
DB，AC=
CB，
∴BC=AD，设BC=AD=5a，AB=4a，AD=5a，
则CD=14a=4cm，
a=
，
AB=4a=
；
故答案为：
或
或14
| 5 |
| 9 |
∴BD=
| 9 |
| 5 |
（1）当B在D的右边时，
有AB=AD+DB=
| 14 |
| 5 |
∵AC=
| 9 |
| 5 |
①当B在C的右边时，
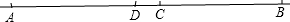
∵此时AB=AC+CB=
| 14 |
| 5 |
∴AD=BC，
∵AC=AD+DC=BC+DC，
| 9 |
| 5 |
即BC=5，
∴AB=14
②当B在C的左边时，
有AB=AC-BC=
| 9 |
| 5 |
| 4 |
| 5 |
∵AD=
| 5 |
| 9 |
∴
| AD |
| BC |
| 2 |
| 7 |
∵DC=DB+BC=DB+
| 7 |
| 2 |
| 9 |
| 5 |
| 7 |
| 2 |
解得AD=
| 40 |
| 53 |
AB=
| 112 |
| 53 |
（2）同理当B在D的左边时，
∵AD=
| 5 |
| 9 |
| 9 |
| 5 |
∴BC=AD，设BC=AD=5a，AB=4a，AD=5a，
则CD=14a=4cm，
a=
| 2 |
| 7 |
AB=4a=
| 8 |
| 7 |
故答案为：
| 8 |
| 7 |
| 112 |
| 53 |
点评：本题考查了求两点之间的距离的应用，主要考查学生的计算能力．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
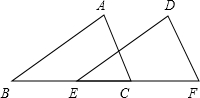已知：如图，同一直线上有四点B、E、C、F，且 AB∥DE，AC∥DF，BE=CF．
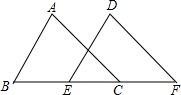已知：如图，同一直线上有四点B、E、C、F，且∠A=∠D，∠B=∠DEF，BE=CF．