题目内容
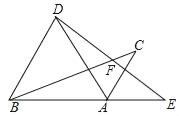
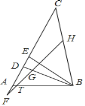
【题目】如图,在△ABC中,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②∠BEF=![]() (∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=
(∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=![]() (∠BAC﹣∠C);其中正确的是_____.
(∠BAC﹣∠C);其中正确的是_____.
【答案】①②③④
【解析】
①根据BD⊥FD,FH⊥BE和∠FGD=∠BGH,证明结论正确;
②根据角平分线的定义和三角形外角的性质证明结论正确;
③根据垂直的定义和同角的余角相等的性质证明结论正确;
④证明∠DBE=∠BAC-∠C,根据①的结论,证明结论正确.
解:①∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,
故①正确;
②∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
∴∠BEF=![]() (∠BAF+∠C),
(∠BAF+∠C),
故②正确;
③∵∠AEB=∠EBC+∠C,
∵∠ABE=∠EBC,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=90![]() -∠DFH,∠AEB=90
-∠DFH,∠AEB=90![]() -∠DFH,
-∠DFH,
∴∠FGD=∠AEB
∴∠FGD=∠ABE+∠C.
故③正确;
④∠ABD=90°-∠BAC,
∠DBE=∠ABE-∠ABD=∠ABE-90°+∠BAC=∠CBD-∠DBE-90°+∠BAC,
∵∠CBD=90°-∠C,
∴∠DBE=∠BAC-∠C-∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC-∠C-∠DBE,
∴∠F=![]() (∠BAC-∠C);
(∠BAC-∠C);
故④正确,
故答案为:①②③④.

练习册系列答案
相关题目