题目内容
 如图,AD是∠BAC的平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F.
如图,AD是∠BAC的平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F.
试说明:EC平分∠DEF.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ACD与△AED中,
∵ ,
,
∴△ACD≌△AED(SAS),
∴CD=ED,
∴∠DEC=∠DCE,
∵EF∥BC,
∴∠FEC=∠DCE,
∴∠DEC=∠FEC,
∴CE平分∠DEF.
分析:先根据SAS证明△ACD≌△AED,再根据全等三角形的性质得到CD=ED,由等腰三角形的性质和平行线的性质可得∠DEC=∠FEC,从而得出结论.
点评:考查了全等三角形的判定与性质,等腰三角形的性质和平行线的性质,解题的关键是SAS证明△ACD≌△AEC.
∴∠BAD=∠CAD,
在△ACD与△AED中,
∵
 ,
,∴△ACD≌△AED(SAS),
∴CD=ED,
∴∠DEC=∠DCE,
∵EF∥BC,
∴∠FEC=∠DCE,
∴∠DEC=∠FEC,
∴CE平分∠DEF.
分析:先根据SAS证明△ACD≌△AED,再根据全等三角形的性质得到CD=ED,由等腰三角形的性质和平行线的性质可得∠DEC=∠FEC,从而得出结论.
点评:考查了全等三角形的判定与性质,等腰三角形的性质和平行线的性质,解题的关键是SAS证明△ACD≌△AEC.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
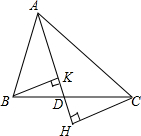 如图,AD是∠BAC的角平分线,交△ABC的边BC于点D,BH⊥AD,CK⊥AD,垂足分别为H、K.
如图,AD是∠BAC的角平分线,交△ABC的边BC于点D,BH⊥AD,CK⊥AD,垂足分别为H、K. 如图,AD是∠BAC的平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F.
如图,AD是∠BAC的平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F.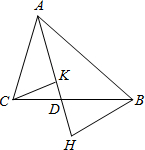 如图,AD是∠BAC的角平分线,交△ABC的边BC于点D,BH⊥AD,CK⊥AD,垂足分别为H、K,你能说明AB•DK=AC•DH吗?
如图,AD是∠BAC的角平分线,交△ABC的边BC于点D,BH⊥AD,CK⊥AD,垂足分别为H、K,你能说明AB•DK=AC•DH吗? 如图,AD是∠BAC的平分线,DE⊥AB于E.若△ABC的面积为45cm2,AB=15cm,AC=12cm,则DE=
如图,AD是∠BAC的平分线,DE⊥AB于E.若△ABC的面积为45cm2,AB=15cm,AC=12cm,则DE=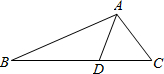 如图,AD是∠BAC的平分线,写出图中相等的角:
如图,AD是∠BAC的平分线,写出图中相等的角: