题目内容
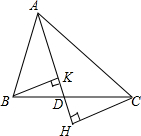如图，AD是∠BAC的角平分线，交△ABC的边BC于点D，BH⊥AD，CK⊥AD，垂足分别为H、K．求证：（1）△CHD∽△BKD；
（2）AB•DH=AC•DK．
分析：（1）求出∠BKD=∠H=90°，∠BDK=∠CDH，根据相似三角形判定推出即可；
（2）根据相似三角形性质得出
=
，证△ABK∽△ACH，得出
=
，推出
=
即可．
（2）根据相似三角形性质得出
| BK |
| CH |
| DK |
| DH |
| AB |
| AC |
| BK |
| CH |
| AB |
| AC |
| DK |
| DH |
解答：证明：（1）∵BH⊥AD，CK⊥AD，
∴∠BKD=∠H=90°，
∵∠BDK=∠CDH，
∴△CHD∽△BKD．
（2）∵△CHD∽△BKD，
∴
=
，
∵BH⊥AD，CK⊥AD，
∴∠AKB=∠H=90°，
∵∠CAH=∠BAK，
∴△ABK∽△ACH，
∴
=
，
∴
=
，
∴AB•DH=AC•BK．
∴∠BKD=∠H=90°，
∵∠BDK=∠CDH，
∴△CHD∽△BKD．
（2）∵△CHD∽△BKD，
∴
| BK |
| CH |
| DK |
| DH |
∵BH⊥AD，CK⊥AD，
∴∠AKB=∠H=90°，
∵∠CAH=∠BAK，
∴△ABK∽△ACH，
∴
| AB |
| AC |
| BK |
| CH |
∴
| AB |
| AC |
| DK |
| DH |
∴AB•DH=AC•BK．
点评：本题考查了相似三角形的性质和判定的应用，主要考查了学生的推理能力．
练习册系列答案
相关题目
如图，AD是∠BAC的平分线，点E在AB上，且AE=AC，EF∥BC交AC于点F．
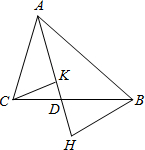如图，AD是∠BAC的角平分线，交△ABC的边BC于点D，BH⊥AD，CK⊥AD，垂足分别为H、K，你能说明AB•DK=AC•DH吗？
如图，AD是∠BAC的平分线，DE⊥AB于E．若△ABC的面积为45cm2，AB=15cm，AC=12cm，则DE=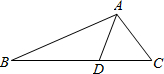
如图，AD是∠BAC的平分线，写出图中相等的角：