题目内容
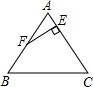
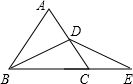
在等边△ABC中，D为AC的中点，E为BC延长线上一点，且DB=DE，若△ABC的周长为12，则△DCE的周长为（ ）
| A．4 | B．4+2
| C．4+
| D．4+2
|
∵△ABC是等边三角形，且D是AC边的中点，
∴BD⊥AC，∠CBD=∠ABD=30°，AB=BC=AC=4
∵BD=DE
∴∠DBC=∠E=30°
∴∠BDE=180°-30°-30°=120°
∵∠BDC=90°
∴∠CDE=∠E=30°
∴CD=CE=
AC=2
直角三角形BCD中，BD=
=
=2
∴DE=BD=2
∴三角形DCE的周长=DC+DE+CE=4+2
．
故选B．
∴BD⊥AC，∠CBD=∠ABD=30°，AB=BC=AC=4
∵BD=DE
∴∠DBC=∠E=30°
∴∠BDE=180°-30°-30°=120°
∵∠BDC=90°
∴∠CDE=∠E=30°
∴CD=CE=
| 1 |
| 2 |
直角三角形BCD中，BD=
| BC2-CD2 |
| 42-22 |
| 3 |
∴DE=BD=2
| 3 |
∴三角形DCE的周长=DC+DE+CE=4+2
| 3 |
故选B．
练习册系列答案
教材全解字词句篇系列答案
相关题目
