题目内容
正实数a1,a2,….,a2011满足a1+a2+…..+a2011=1,设P=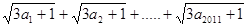 ,则( )
,则( )
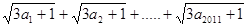 ,则( )
,则( )| A.p>2012 | B.p=2012 |
| C.p<2012 | D.p与2012的大小关系不确定 |
A
分析:利用极值法当a1=1,则其他都为0,得出函数的最小值,进而得出函数取值范围.
解答:解:∵正实数a1,a2,…,a2011满足a1+a2+…+a2011=1,
∴a1,a2,…,a2011中最大数小于等于1,
∵P=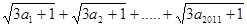 ,要使此式子最小,只要a1,a2,…,a2011其中一个为1即可,
,要使此式子最小,只要a1,a2,…,a2011其中一个为1即可,
∴当a1=1,则其他都为0,
∴P=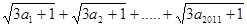 ,
,
=2+1+1+…+1,
=2012,
∵a1,a2,…,a2011中不可能都相等,
∴P>2012.
故选:A.
解答:解:∵正实数a1,a2,…,a2011满足a1+a2+…+a2011=1,
∴a1,a2,…,a2011中最大数小于等于1,
∵P=
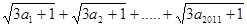 ,要使此式子最小,只要a1,a2,…,a2011其中一个为1即可,
,要使此式子最小,只要a1,a2,…,a2011其中一个为1即可,∴当a1=1,则其他都为0,
∴P=
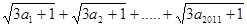 ,
,=2+1+1+…+1,
=2012,
∵a1,a2,…,a2011中不可能都相等,
∴P>2012.
故选:A.

练习册系列答案
相关题目
 ×
×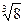 -
-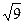 ×
×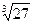
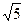 )2-
)2- +
+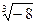
 都是无理数,且
都是无理数,且 ,则
,则 , -
, - ,-3.14,0,
,-3.14,0,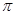 ,
,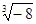 , -0.020020002 , 0.12121121112┄┄ 中,无理数有 【 】
, -0.020020002 , 0.12121121112┄┄ 中,无理数有 【 】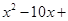 ________=(
________=(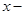 ________)2.
________)2. ,则
,则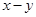 的值是
的值是 

 ,则
,则 ( )
( )


 的值.(6分)
的值.(6分)