题目内容
如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
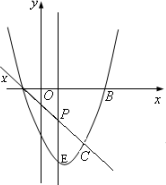
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
答案:
解析:
解析:
|
解:(1)令y=0,解得 ∴A(-1,0)B(3,0); (1分) 将C点的横坐标x=2代入 ∴直线AC的函数解析式是y=-x-1 (2)设P点的横坐标为x(-1≤x≤2)(注:x的范围不写不扣分) 则P、E的坐标分别为:P(x,-x-1), (1分) E( ∵P点在E点的上方,PE= ∴当 (3)存在4个这样的点F,分别是 (结论“存在”给1分,4个做对1个给1分,过程酌情给分) |

练习册系列答案
相关题目

 x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
 x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .

 AB时,求点E的坐标;
AB时,求点E的坐标; 的交点A的横坐标是1,则关于x的不等式
的交点A的横坐标是1,则关于x的不等式