题目内容
如图,抛物线y=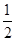 x2-
x2-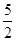 x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
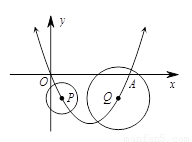
(1)点Q的横坐标是 (用含t的代数式表示);
(2)若⊙P与⊙Q 相离,则t的取值范围是 .
【答案】
(1)5-t;(2)0≤t<1,2<t≤ .
.
【解析】
试题分析:(1)如图,抛物线y= x2-
x2- x与x轴交于O,A两点,两圆刚开始分别在O,A点,所以
x与x轴交于O,A两点,两圆刚开始分别在O,A点,所以 ;设点P的横坐标为t,所以点Q的横坐标=5-t
;设点P的横坐标为t,所以点Q的横坐标=5-t
(2)若⊙P与⊙Q 相离,所以两圆的圆心距大于两圆的半径之和,即5-t-t>1+2,解得t<1;由题知点P的横坐标为t,刚开始P在原点,所以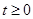 ,因此0≤t<1;当⊙P与⊙Q相切后再相离时,也就是第二次相离,⊙Q在左,⊙P在右,即t-(5-t)>1-2,解得t>2; 当运动到P,Q两点重合时同时停止运动,t
,因此0≤t<1;当⊙P与⊙Q相切后再相离时,也就是第二次相离,⊙Q在左,⊙P在右,即t-(5-t)>1-2,解得t>2; 当运动到P,Q两点重合时同时停止运动,t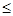 5-t,解得
5-t,解得 ,所以t的取值范围0≤t<1,2<t≤
,所以t的取值范围0≤t<1,2<t≤
考点:二次函数和圆
点评:本题考查二次函数和圆,掌握二次函数的性质和圆相离,会判断两圆相离,圆心距与两圆半径之间的关系是本题关键

练习册系列答案
相关题目
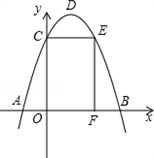
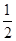 x2-
x2- x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .
x与x轴交于O,A两点. 半径为1的动圆(⊙P),圆心从O点出发沿抛物线向靠近点A的方向移动;半径为2的动圆(⊙Q),圆心从A点出发沿抛物线向靠近点O的方向移动. 两圆同时出发,且移动速度相等,当运动到P,Q两点重合时同时停止运动. 设点P的横坐标为t .

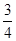 AB时,求点E的坐标;
AB时,求点E的坐标;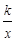 的交点A的横坐标是1,则关于x的不等式
的交点A的横坐标是1,则关于x的不等式