题目内容
【题目】(1)请你根据下面画图要求,在图①中完成画图操作并填空.
如图①,△ABC中,∠BAC=30°,∠ACB=90°,∠PAM=∠A.
操作:(1)延长BC.
(2)将∠PAM绕点A逆时针方向旋转60°后,射线AM交BC的延长线于点D.
(3)过点D作DQ∥AB.
(4)∠PAM旋转后,射线AP交DQ于点G.
(5)连结BG.
结论:![]() = .
= .
(2)如图②,△ABC中,AB=AC=1,∠BAC=36°,进行如下操作:将△ABC绕点A按逆时针方向旋转α度角,并使各边长变为原来的n倍(n>1),得到△AB′C′.当点B、C、B′在同一条直线上,且四边形ABB′C′为平行四边形时(如图③),求a和n的值.

【答案】(1)![]() ;(2)72°;2.62.
;(2)72°;2.62.
【解析】
试题分析:(1)根据旋转得出△ABC~△AGD,设AB为2,根据30°的直角三角形的性质得出AD=2![]() ,进一步得出AG=4,可得
,进一步得出AG=4,可得![]() ;
;
(2)由四边形ABB′C′是平行四边形,易求得a=36°,又由△ABC∽△AB′C′,根据相似三角形的对应边成比例,继而求得答案.
试题解析:(1)如图:
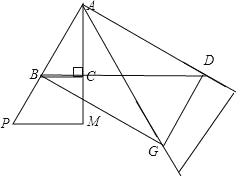
∵∠BAC=30°,∠ACB=90°,
∴∠PAM=∠A=30°,
∵∠PAM绕点A逆时针方向旋转60°,
∴∠BAG=60°,△ABC~△AGD,
∴∠GAD=∠BAC=∠MAG=30°,
∴△BAD是Rt△,∠ABD=60°,
∴∠ADB=30°,
设AB为2,则可得AD=![]() ,
,
∵DQ∥AB,∠BAD=90°
∴∠ADG=90°,
∵∠GAD=30°,AD=![]() ,
,
∴AG=4,
∴![]() ;
;
(2)∵四边形ABB′C′是平行四边形,
∴AC′∥BB′,
又∵∠BAC=36°,AB=AC
∴∠ABC=72°.
∴∠B′AC′=∠BAC=36°,
∴∠CAB′=36°,
∴α=180°-72°-36°=72°;
∴∠B′AC′=∠BAC=36°,而∠B=∠AB′C′,
∴△ABC∽△AB′C′,
∴AB:BB′=CB:AB,
∴AB2=CBAB′,
而 AB=1,
BC=2ABsin18°≈0.618,
所以可得n=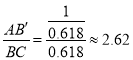 .
.

 寒假学与练系列答案
寒假学与练系列答案

