��Ŀ����
����Ŀ��������y=ax2+bx+3������A��1��0���͵�B��5��0����
��1���������������Ӧ�ĺ�������ʽ��
��2������������ֱ��![]() �ཻ��C��D���㣬��P���������ϵĶ�����λ��x���·���ֱ��PM��y�ᣬ�ֱ���x���ֱ��CD���ڵ�M��N��
�ཻ��C��D���㣬��P���������ϵĶ�����λ��x���·���ֱ��PM��y�ᣬ�ֱ���x���ֱ��CD���ڵ�M��N��
������PC��PD����ͼ1���ڵ�P�˶������У���PCD������Ƿ�������ֵ�������ڣ����������ֵ���������ڣ�˵�����ɣ�
������PB������C��CQ��PM������Ϊ��Q����ͼ2���Ƿ���ڵ�P��ʹ����CNQ����PBM���ƣ������ڣ�������������ĵ�P�����ꣻ�������ڣ�˵�����ɣ�

���𰸡���1��![]() ����2����
����2����![]() ������������2��
������������2��![]() ����
����![]() ��
��![]() ��.
��.
��������
�����������1����A��B��������꣬���ô���ϵ��������������߽���ʽ��
��2���������P�����꣬��ɱ�ʾ��M��N�����꣬����ֱ���������߽���ʽ�����C��D�����꣬��C��D��PN�Ĵ��ߣ�����t��ʾ����PCD����������ö��κ��������ʿ���������ֵ��
������CNQ����PBM����ʱ��![]() ��
��![]() �������������P�����꣬�ɷֱ��ʾ���߶εij����ɵõ�����P������ķ��̣������P�����꣮
�������������P�����꣬�ɷֱ��ʾ���߶εij����ɵõ�����P������ķ��̣������P�����꣮
�����������1����������y=ax2+bx+3������A��1��0���͵�B��5��0����
��![]() �����
�����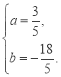
���������߶�Ӧ�ĺ�������ʽΪ![]() ��
��
��2���١���P���������ϵĶ�����λ��x���·���
������P��t��![]() ����1��t��5����
����1��t��5����
��ֱ��PM��y�ᣬ�ֱ���x���ֱ��CD���ڵ�M��N��
��M��t��0����N��t��![]() ����
����
��PN=![]() .
.
����ֱ��CD�������߽���ʽ�ɵ�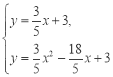 �����
�����![]() ��
��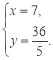 ��
��
��C��0��3����D��7��![]() ����
����
�ֱ��C��D��ֱ��PN��ֱ�ߣ�����ֱ�ΪE��F����ͼ1��
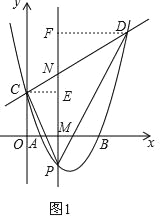
��CE=t��DF=7��t��
��S��PCD=S��PCN+S��PDN=![]() PN��CE+
PN��CE+![]() PNDF=
PNDF=![]() PN=
PN=![]()
![]() ��
��
����t=![]() ʱ����PCD����������ֵ�����ֵΪ
ʱ����PCD����������ֵ�����ֵΪ![]() ��
��
�����ڣ�
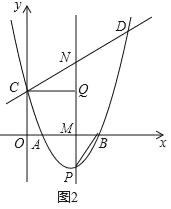
�ߡ�CQN=��PMB=90�㣬
������CNQ����PBM����ʱ����![]() ��
��![]() ���������
���������
��CQ��PM������ΪQ��
��Q��t��3������C��0��3����N��t��![]() ����
����
��CQ=t��NQ=![]() ��3=
��3=![]() ��
��
��![]() ��
��
��P��t��![]() ����M��t��0����B��5��0����
����M��t��0����B��5��0����
��BM=5��t��PM=0����![]() ��=
��=![]() ��
��
��![]() ʱ����PM=
ʱ����PM=![]() BM����
BM����![]()
![]() �����t=2��t=5����ȥ������ʱP��2��
�����t=2��t=5����ȥ������ʱP��2��![]() ����
����
��![]() ʱ����BM=
ʱ����BM=![]() PM����5��t=
PM����5��t=![]() ��
��![]() �������t=
�������t=![]() ��t=5����ȥ������ʱP��
��t=5����ȥ������ʱP��![]() ��
��![]() ����
����
���Ͽ�֪�������������ĵ�P��������ΪP��2��![]() ����
����![]() ��
��![]() ����
����

 ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д�����Ŀ��ij��ѧŮ�������15����Ա������������±���
���䣨�꣩ | 13 | 14 | 15 | 16 |
��Ա���ˣ� | 2 | 3 | 6 | 4 |
��֧��Ӷ�Ա���������������λ���ֱ��ǣ�������
A.14��15
B.14��14.5
C.15��15
D.15��14
����Ŀ�� ������![]() ��ѧ���μ�ѧУ���е�����ϧ������Զ�붾Ʒ��ֻ�Ǿ�������������Գɼ����з������������µ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��δ��ɣ�.����
��ѧ���μ�ѧУ���е�����ϧ������Զ�붾Ʒ��ֻ�Ǿ�������������Գɼ����з������������µ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ��δ��ɣ�.����![]() ��ѧ���ɼ���δͳ�ƣ���
��ѧ���ɼ���δͳ�ƣ���![]() ��ѧ���ɼ����£�
��ѧ���ɼ����£�![]() .
.
Ƶ���ֲ���
������ | Ƶ���������� |
|
|
|
|
|
|
|
|

�����������⣺
�����Ƶ���ֲ�����![]() ��
��![]() ��
��
����ȫƵ���ֲ�ֱ��ͼ��
��ȫУ����![]() ��ѧ���μӳ��������Ƹ�У�ɼ�
��ѧ���μӳ��������Ƹ�У�ɼ�![]() ��Χ�ڵ�ѧ���ж����ˣ�
��Χ�ڵ�ѧ���ж����ˣ�
��������ס��ҡ�����λͬѧ�ijɼ����е�һ����ѡ���˲μӾ�������ǡ��ѡ�мס�����λͬѧ�ĸ���.
