题目内容
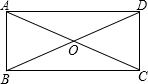如图，矩形ABCD的周长为30，对角线AC和BD相交于点O，若△DOC的周长比△BOC的周长少3，求矩形ABCD的面积．考点：矩形的性质
专题：
分析：由矩形的性质和条件若△DOC的周长比△BOC的周长少3，可知BC-DC=3，再根据条件矩形ABCD的周长为30，可得CD+BC=15，进而求出AD和BC的长，利用矩形的面积公式即可求出矩形ABCD的面积．
解答：解：∵四边形ABCD是矩形，
∴AO=CO，
∵△DOC的周长比△BOC的周长少3，
∴BC-CD=3，
∵矩形ABCD的周长为30，
∴CD+BC=15，
∴BC=9，C=6，
∴矩形ABCD的面积=9×6=54．
∴AO=CO，
∵△DOC的周长比△BOC的周长少3，
∴BC-CD=3，
∵矩形ABCD的周长为30，
∴CD+BC=15，
∴BC=9，C=6，
∴矩形ABCD的面积=9×6=54．
点评：本题考查了矩形的性质：对角线相等且互相平分以及矩形面积公式的运用，题目难度不大．
练习册系列答案
相关题目
甲、乙两人赛跑时，路程s（m）和时间t（s）的关系如图所示，请你观察图象并回答：
为了解九年级学生体能情况，随机抽查了其中的40名学生，测试了1分钟仰卧起坐的次数，并绘制成如图的频数分布直方图，则仰卧起坐的次数在20～25次之间的频率是