题目内容
 甲、乙两人赛跑时,路程s(m)和时间t(s)的关系如图所示,请你观察图象并回答:
甲、乙两人赛跑时,路程s(m)和时间t(s)的关系如图所示,请你观察图象并回答:(1)这次赛跑的长度有多少米?
(2)甲、乙两人中谁最先到达终点?
(3)计算出甲、乙在这次比赛中的速度.
(4)写出甲、乙在这次赛跑路程s(m)和时间t(s)的函数关系式及自变量t的取值范围.
考点:一次函数的应用
专题:
分析:(1)根据函数图象,甲、乙二人路程的最大值为100米解答;
(2)根据二人到达100米的时间确定先到达终点的选手;
(3)根据速度=路程÷时间,分别列式计算即可得解;
(4)根据二人的速度分别写出函数关系式即可.
(2)根据二人到达100米的时间确定先到达终点的选手;
(3)根据速度=路程÷时间,分别列式计算即可得解;
(4)根据二人的速度分别写出函数关系式即可.
解答:解:(1)由图可知,这次赛跑的长度是100米;
(2)∵甲12秒到达终点,乙12.5秒到达终点,
∴甲先到达终点;
(3)甲速度:100÷12=
米/秒,
乙速度:100÷12.5=8米/秒;
(4)甲:s=
t(0≤t≤12),
乙:s=8t(0≤t≤12.5).
(2)∵甲12秒到达终点,乙12.5秒到达终点,
∴甲先到达终点;
(3)甲速度:100÷12=
| 25 |
| 3 |
乙速度:100÷12.5=8米/秒;
(4)甲:s=
| 25 |
| 3 |
乙:s=8t(0≤t≤12.5).
点评:本题考查了一次函数的应用,主要是在直角坐标系中的读图能力的考查,路程、速度、时间三者之间的关系.

练习册系列答案
相关题目
 已知,如图:在△ABC中,AD⊥BC于D,AB=6,AC=4,BC=8,求BD、DC的长.
已知,如图:在△ABC中,AD⊥BC于D,AB=6,AC=4,BC=8,求BD、DC的长. 如图,矩形ABCD的周长为30,对角线AC和BD相交于点O,若△DOC的周长比△BOC的周长少3,求矩形ABCD的面积.
如图,矩形ABCD的周长为30,对角线AC和BD相交于点O,若△DOC的周长比△BOC的周长少3,求矩形ABCD的面积. 如图所示,已知等腰△ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm.
如图所示,已知等腰△ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm.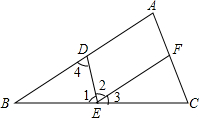 如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,求证:∠A+∠B+∠C=180°.
如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,求证:∠A+∠B+∠C=180°.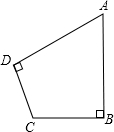 如图,∠A=60°,∠B=∠D=90°,BC=4,CD=3.求AD的长.
如图,∠A=60°,∠B=∠D=90°,BC=4,CD=3.求AD的长.